题目内容
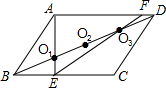
如图，在平行四边形ABCD中，O1、O2、O3分别是对角线BD上的三点，且BO1=O1O2=O2O3=O3D，连接AO1并延长交BC于点E，连接EO3并延长交AD于点F，则AF：DF等于（ ）
| A．19：2 | B．9：1 | C．8：1 | D．7：1 |
根题意，在平行四边形ABCD中，
易得△BO3E∽△DO3F
∴BE：FD=3：1
∵△BO1E∽△DO1A
∴BE：AD=1：3
∴AD：DF=9：1
∴AF：DF=（AD-FD）：DF=（9-1）：1=8：1
故选C．
易得△BO3E∽△DO3F
∴BE：FD=3：1
∵△BO1E∽△DO1A
∴BE：AD=1：3
∴AD：DF=9：1
∴AF：DF=（AD-FD）：DF=（9-1）：1=8：1
故选C．
练习册系列答案
相关题目
E．根据以上条件写出三个正确结论（除AB=AC，AO=BO，∠ABC=∠ACB外）是：
