题目内容
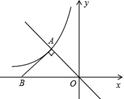
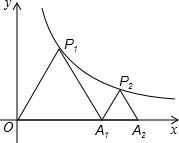
如图,P1是反比例函数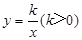 在第一象限图象上的一点,已知△P1O A1为等边三角形,点A1的坐标为(2,0).
在第一象限图象上的一点,已知△P1O A1为等边三角形,点A1的坐标为(2,0).
(1)直接写出点P1的坐标;
(2)求此反比例函数的解析式;
(3)若△P2A1A2为等边三角形,求点A2的坐标.
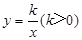 在第一象限图象上的一点,已知△P1O A1为等边三角形,点A1的坐标为(2,0).
在第一象限图象上的一点,已知△P1O A1为等边三角形,点A1的坐标为(2,0).
(1)直接写出点P1的坐标;
(2)求此反比例函数的解析式;
(3)若△P2A1A2为等边三角形,求点A2的坐标.
(1)P1(1,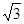 );(2)
);(2)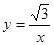 ;(3)(
;(3)( ,0).
,0).
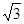 );(2)
);(2)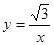 ;(3)(
;(3)( ,0).
,0).试题分析:(1)由于△P1OA1为等边三角形,作P1C⊥OA1,垂足为C,由等边三角形的性质及勾股定理可求出点P1的坐标;
(2)根据点P1是反比例函数y=
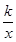 (k>0)图象上的一点,利用待定系数法求出此反比例函数的解析式;
(k>0)图象上的一点,利用待定系数法求出此反比例函数的解析式;(3)作P2D⊥A1A2,垂足为D.设A1D=a,由于△P2A1A2为等边三角形,由等边三角形的性质及勾股定理,可用含a的代数式分别表示点P2的横、纵坐标,再代入反比例函数的解析式中,求出a的值,进而得出A2点的坐标.
试题解析:(1)P1(1,
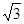 );
);(2)∵P1在反比例函数
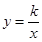 (
(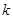 >0)图象上,∴
>0)图象上,∴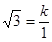 ,
,∴
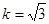 ,
,∴反比例函数的解析式为
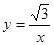 ;
;(3)设等边三角形P2 A1 A2的边长为a(a>0),则A2(2+a,0).
如图,过P2作P2H⊥x轴,垂足为点H.
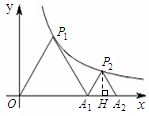
∴A1H=
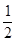 a,P2H= P2 A1sin∠P2A1H=a·sin600=
a,P2H= P2 A1sin∠P2A1H=a·sin600=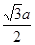 ,
,∴P2(2+
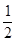 a,
a,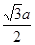 ).
). ∵ P2在反比例函数
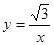 图象上,∴
图象上,∴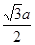 =
=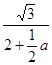 ,
, 即
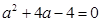 ,解得:
,解得: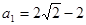 ,
,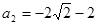 (舍去)
(舍去)∴2+a=
 ,∴A2(
,∴A2( ,0)
,0)考点: 反比例函数综合题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
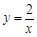 (x>0)上,点B在双曲线
(x>0)上,点B在双曲线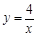 (x>0)上,且AB//
(x>0)上,且AB// 轴,点P是
轴,点P是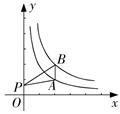
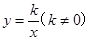 在第一象限内的交点.
在第一象限内的交点.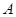 的坐标及
的坐标及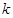 的值;
的值;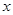 轴上确定一点
轴上确定一点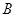 ,使
,使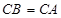 ,求出点
,求出点 (x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:①菱形OABC的面积为80; ②E点的坐标是(4,8);③双曲线的解析式为y=
(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:①菱形OABC的面积为80; ②E点的坐标是(4,8);③双曲线的解析式为y= (x>0); ④
(x>0); ④ ,其中正确的结论有( )个。
,其中正确的结论有( )个。
 分别与双曲线
分别与双曲线 和直线
和直线 交于D、A两点,过点A、D分别作x轴的垂线段,垂足为点B、C.若四边形ABCD是正方形,则a的值为 .
交于D、A两点,过点A、D分别作x轴的垂线段,垂足为点B、C.若四边形ABCD是正方形,则a的值为 .
 的图象,如图所示,则
的图象,如图所示,则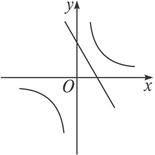
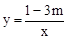 的图象上有两点A
的图象上有两点A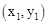 ,B
,B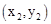 ,当
,当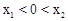 时,有
时,有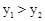 ,则m的取值范围是
,则m的取值范围是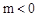
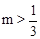
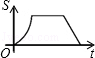
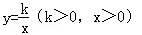 上的两点,BC∥x轴,交y轴于C,动点P从坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过运动路线上任意一点P作PM⊥x轴于M,PN⊥y轴于N,设四边形OMPN的面积为S,P点运动的时间为t,则S关于t的函数图象大致是( )
上的两点,BC∥x轴,交y轴于C,动点P从坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过运动路线上任意一点P作PM⊥x轴于M,PN⊥y轴于N,设四边形OMPN的面积为S,P点运动的时间为t,则S关于t的函数图象大致是( )
 B
B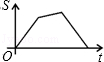 C
C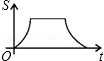 D
D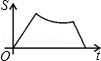
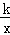 在第二象限的交点,AB⊥OA交x轴于点B,△AOB的面积为4,则k的值是_____________.
在第二象限的交点,AB⊥OA交x轴于点B,△AOB的面积为4,则k的值是_____________.