题目内容
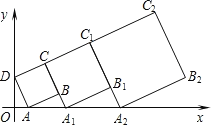
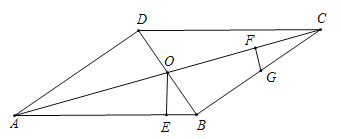
【题目】在平行四边形![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,
,![]() 点
点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;同时,点
;同时,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;当一个点停止运动时,另一个点也停止运动.连接
;当一个点停止运动时,另一个点也停止运动.连接![]() ,过点
,过点![]() 作
作![]() ,设运动时间为
,设运动时间为![]() ,解答下列问题:
,解答下列问题:
(1)当![]() 为何值时
为何值时![]() ;
;
(2)在运动过程中,是否存在某一时刻![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)当![]() 为何值时
为何值时![]() 是等腰三角形?
是等腰三角形?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]()
【解析】
(1)由已知易得![]() ,要求
,要求![]() ,只要
,只要![]() 即可.根据相似三角形性质列式计算即可.
即可.根据相似三角形性质列式计算即可.
(2)由图可知![]() ,根据平行四边形面积可求
,根据平行四边形面积可求![]() ,
,![]() ,进而用t表示出
,进而用t表示出![]() 的面积;再由
的面积;再由![]() ,由相似三角形的面积比可求得
,由相似三角形的面积比可求得![]() 的面积,从而根据
的面积,从而根据![]() 列方程即可解答;
列方程即可解答;
(3)分三种情况讨论,当![]() 、
、![]() 、
、![]() 时,分别根据等腰三角形三线合一性质和相似三角形性质,由比例式列方程求解即可.
时,分别根据等腰三角形三线合一性质和相似三角形性质,由比例式列方程求解即可.
解:(1)∵![]()
∴![]()
∴![]()
∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]()
∴![]() ;
;
(2)由(1)可知![]() ,
,
∴![]() ,
,![]()
∴![]() ,
,
又∵![]()
∴![]() ,
,
∴![]() ,
,
∴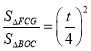 ,
,
∴![]() ,
,
∴![]() ,
,
当![]() 时,即
时,即![]() ,
,
即![]()
解得:![]() ,
,![]() (舍)
(舍)
所以当![]() 时,
时,![]() ;
;
(3)①当![]() 时,
时,
![]() ;
;
②当![]() 时,过O点作OG⊥AB,如图:
时,过O点作OG⊥AB,如图:
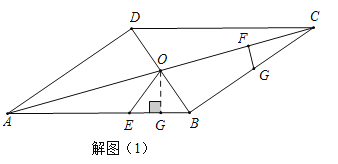
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
即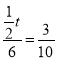 ,
,
解得:![]() ;
;
③当![]() 时,
时,
过![]() 作
作![]() 于
于![]() ,
,

则![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即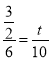 ,
,
∴![]() ,
,
所以当![]() 或
或![]() 或
或![]() 时,
时,![]() 是等腰三角形.
是等腰三角形.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目