��Ŀ����
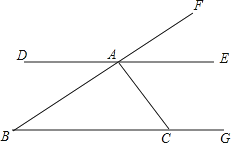
����Ŀ����ͼ��1����ֱ��![]() ��
��![]() ���ڵ�P��Rt��ABC�У�б��AB=5��ֱ�DZ�AC=3����A��0��
���ڵ�P��Rt��ABC�У�б��AB=5��ֱ�DZ�AC=3����A��0�� ![]() ����
����![]() �����˶���ֱ�DZ�BC��ֱ��
�����˶���ֱ�DZ�BC��ֱ��![]() �ϣ�����ABC�Ƶ�P˳ʱ����ת90�㣬�õ���DEF����ֱ��
�ϣ�����ABC�Ƶ�P˳ʱ����ת90�㣬�õ���DEF����ֱ��![]() Ϊ�Գ���������߾�����F��
Ϊ�Գ���������߾�����F��
��1�����F�����꣨�ú�![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��
��2������ͼ��2���������ߵĶ���Ϊ��Cʱ��������ǡ�ù�����ԭ�㡣���ʱ�����ߵĽ���ʽ��
����ͼ��3�����ı���������ߵĿ��ڷ������״���õ�A��λ�÷����仯��ʹ���������߶�ABʼ���н���M��![]() ��
�� ![]() ��.
��.
(��)��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�������仯�����У���![]() ���ijһ��ֵʱ����A��λ��Ψһȷ�������ʱ��M�����ꡣ
���ijһ��ֵʱ����A��λ��Ψһȷ�������ʱ��M�����ꡣ


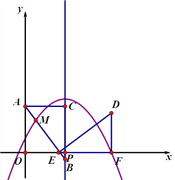
ͼ��1�� ͼ��2�� ͼ��3��
���𰸡���1����F������Ϊ��![]() ��0������2����
��0������2����![]() ���ڣ�����
���ڣ����� ![]() ����ii����M������Ϊ��
����ii����M��������![]() ��
�� ![]() ��
��
����������1������ת��֪��PF=PC=|t |����![]() t
t![]() ʱ��OF=OP+PF=t+3
ʱ��OF=OP+PF=t+3![]() ����֪F��t+3
����֪F��t+3![]() ��0����
��0����
��![]() ʱ��OF=OP��PF=
ʱ��OF=OP��PF= ![]() ����F����Ϊ��
����F������![]() ��0���� ��
��0���� ��![]() ʱ��OF= PF��OP=
ʱ��OF= PF��OP=![]() ����F������Ϊ��F����Ϊ��
����F��������F������![]() ��0��
��0��
���F��������![]() ��0��
��0��
��2�����������ߵĶԳ��Կ�֪��PF=PO=3��������תPC=PF���ʴ�ʱ��C����Ϊ��3��3�����������ߵĽ���ʽΪ![]() ����ԭ���������ɵã�
����ԭ���������ɵã� ![]()
���ʱ�����ߵĽ���ʽΪ![]()
��������������״�ͶԳ�������ı䣬�ʿ��������߽���ʽΪ![]() �����������߹���F��
�����������߹���F��![]() ��0��������ɵã�
��0��������ɵã� ![]() ������ʱ������Ϊ
������ʱ������Ϊ![]()
�����������B������3�� ![]() ��������
��������![]() �����B���������߶����·���ֻ�е�A���������ϻ��Ϸ������������߶�AB���н��㡣
�����B���������߶����·���ֻ�е�A���������ϻ��Ϸ������������߶�AB���н��㡣
��![]() ��0��ʼ����ʱ��PF������������
��0��ʼ����ʱ��PF������������![]() ����߽��������ƶ�����������
����߽��������ƶ�����������![]() �ύ����֮���ƣ���M�����A��£���������߹���Aʱ��
�ύ����֮���ƣ���M�����A��£���������߹���Aʱ�� ![]() ȡ�����ֵ������
ȡ�����ֵ������![]() ��0��ʼ��Сʱ��F��O��P֮�䣬��������������
��0��ʼ��Сʱ��F��O��P֮�䣬��������������![]() �ļ�С�����ƶ�������A�����ƶ����ʵ�M�����A��£���ʵ������߾�����Aʱ��
�ļ�С�����ƶ�������A�����ƶ����ʵ�M�����A��£���ʵ������߾�����Aʱ�� ![]() ȡ����Сֵ������A������������ߣ��ã�
ȡ����Сֵ������A������������ߣ��ã� ![]()
��![]() ��
��
����������AB����ʽΪ![]() ������M�������ֱ���������߽���ʽ�ɵã�
������M�������ֱ���������߽���ʽ�ɵã�
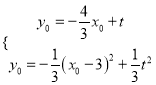 ��ȥ
��ȥ![]() ��������ã�
��������ã� ![]() ��
��
���ڵ�![]() ���ijһ��ֵʱ����A��λ��Ψһȷ����������������
���ijһ��ֵʱ����A��λ��Ψһȷ����������������![]() �ķ�����������ȵ�ʵ�������Ӷ��У�
�ķ�����������ȵ�ʵ�������Ӷ��У�
![]() ��
�� ![]()
��ã� ![]() ��
��![]() ��ȥ��
��ȥ��
����AB����ʽ![]() ���ɵã�
���ɵã� ![]()
���ԣ���ʱ��M������Ϊ��![]() ��
�� ![]() ��
��
���㾦���������ڶ��κ����ۺ��⣬�漰��֪ʶ�У����κ��������ʣ�����ϵ����ȷ�������߽���ʽ�����κ�������ֵ��һԪ���η��̵��б�ʽ���������մ���ϵ�����ǽⱾ��Ĺؼ�������ʱҪע���÷�������˼�룮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�