题目内容
【题目】在一个不透明的袋子中装有仅颜色不同的5个小球,其中红球3个,黑球2个.
⑴先从袋中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,填空:若A为必然事件,则m的值为_______,若A为随机事件,则m的取值为______;
⑵若从袋中随机摸出2个球,正好红球、黑球各1个,用列表法与树状图法求这个事件的概率.
【答案】(1)3,2;(2)![]()
【解析】试题解析:(1)由在一个不透明的袋子中装有仅颜色不同的5个小球,其中红球3个,黑球2个,根据必然事件与随机事件的定义,即可求得答案;(2)根据题意画出树状图,然后由树状图求得所有等可能的结果与从袋中随机摸出2个球,正好红球、黑球各1个的情况,再利用概率公式即可求得答案.
试题解析:
(1)∵“摸出黑球”为必然事件, ∴m=3,
∵“摸出黑球”为随机事件,且m>1, ∴m=2;
故答案为:3,2;
(2)画树状图得:
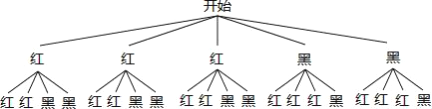
∵共有20种等可能的结果,从袋中随机摸出2个球,正好红球、黑球各1个的有12种情况,
∴从袋中随机摸出2个球,正好红球、黑球各1个的概率为:![]() =
=![]() .
.

练习册系列答案
相关题目




