题目内容
如图,点 为
为 轴正半轴上一点,
轴正半轴上一点, 两点关于
两点关于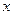 轴对称,过点
轴对称,过点 任作直线交抛物线
任作直线交抛物线 于
于 ,
, 两点
两点

(1)求证:∠ =∠
=∠ ;
;
(2)若点 的坐标为(0,1),且∠
的坐标为(0,1),且∠ =60º,试求所有满足条件的直线
=60º,试求所有满足条件的直线 的函数解析式.
的函数解析式.
 为
为 轴正半轴上一点,
轴正半轴上一点, 两点关于
两点关于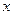 轴对称,过点
轴对称,过点 任作直线交抛物线
任作直线交抛物线 于
于 ,
, 两点
两点
(1)求证:∠
 =∠
=∠ ;
;(2)若点
 的坐标为(0,1),且∠
的坐标为(0,1),且∠ =60º,试求所有满足条件的直线
=60º,试求所有满足条件的直线 的函数解析式.
的函数解析式. 解:(1)如图,分别过点 作
作 轴的垂线,垂足分别为
轴的垂线,垂足分别为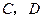 .
.
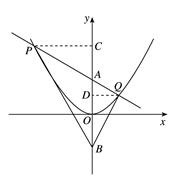
设点 的坐标为(0,
的坐标为(0,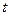 ),则点
),则点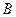 的坐标为(0,-
的坐标为(0,-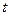 ).
).
设直线 的函数解析式为
的函数解析式为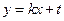 ,并设
,并设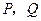 的坐标分别为
的坐标分别为 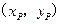 ,
,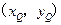 .由
.由
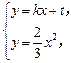
得 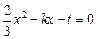 ,于是
,于是 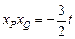 ,即
,即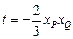 .
.
于是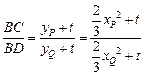
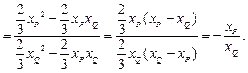
又因为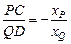 ,所以
,所以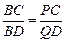 .
.
因为∠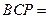 ∠
∠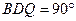 ,所以△
,所以△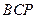 ∽△
∽△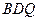 ,
,
故∠ =∠
=∠ .
.
(2) 设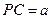 ,
,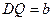 ,不妨设
,不妨设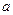 ≥
≥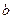 >0,由(1)可知
>0,由(1)可知
∠ =∠
=∠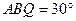 ,
,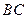 =
=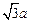 ,
,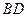 =
=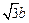 ,
,
所以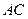 =
=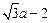 ,
,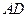 =
=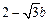 .
.
因为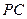 ∥
∥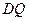 ,所以△
,所以△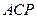 ∽△
∽△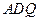 .
.
于是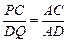 ,即
,即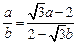 ,
,
所以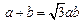 .
.
由(1)中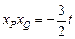 ,即
,即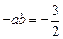 ,所以
,所以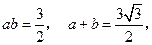
于是可求得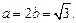
将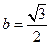 代入
代入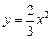 ,得到点
,得到点 的坐标(
的坐标(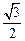 ,
,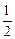 ).
).
再将点 的坐标代入
的坐标代入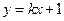 ,求得
,求得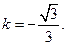
所以直线 的函数解析式为
的函数解析式为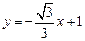 .
.
根据对称性知,所求直线 的函数解析式为
的函数解析式为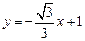 ,或
,或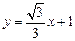 .
.
 作
作 轴的垂线,垂足分别为
轴的垂线,垂足分别为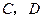 .
.
设点
 的坐标为(0,
的坐标为(0,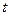 ),则点
),则点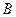 的坐标为(0,-
的坐标为(0,-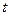 ).
).设直线
 的函数解析式为
的函数解析式为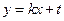 ,并设
,并设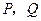 的坐标分别为
的坐标分别为 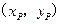 ,
,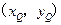 .由
.由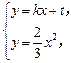
|
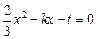 ,于是
,于是 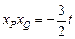 ,即
,即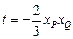 .
. 于是
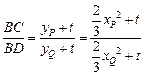
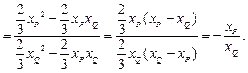
又因为
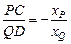 ,所以
,所以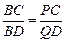 .
.因为∠
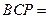 ∠
∠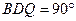 ,所以△
,所以△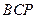 ∽△
∽△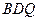 ,
,故∠
 =∠
=∠ .
.(2) 设
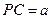 ,
,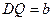 ,不妨设
,不妨设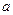 ≥
≥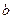 >0,由(1)可知
>0,由(1)可知∠
 =∠
=∠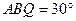 ,
,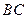 =
=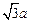 ,
,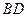 =
=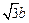 ,
, 所以
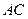 =
=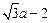 ,
,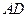 =
=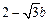 .
.因为
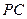 ∥
∥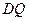 ,所以△
,所以△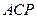 ∽△
∽△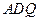 .
.于是
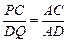 ,即
,即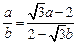 ,
,所以
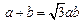 .
.由(1)中
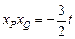 ,即
,即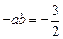 ,所以
,所以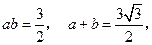
于是可求得
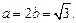
将
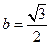 代入
代入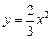 ,得到点
,得到点 的坐标(
的坐标(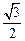 ,
,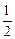 ).
). 再将点
 的坐标代入
的坐标代入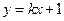 ,求得
,求得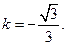
所以直线
 的函数解析式为
的函数解析式为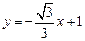 .
.根据对称性知,所求直线
 的函数解析式为
的函数解析式为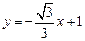 ,或
,或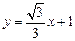 .
.略

练习册系列答案
相关题目

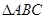 ∽
∽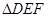 ,
,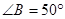 ,
,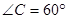 ,则
,则 的度数为 .
的度数为 .
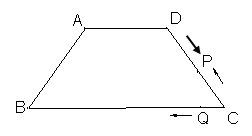
 ,把△BCE沿折痕EC向上翻折,若点B恰好落在AD边上,设这个点为F,则(1)AB= ▲ ,BC= ▲ ;(2)若⊙O内切于以F、E、B、C为顶点的四边形,则⊙O的面积= ▲ .
,把△BCE沿折痕EC向上翻折,若点B恰好落在AD边上,设这个点为F,则(1)AB= ▲ ,BC= ▲ ;(2)若⊙O内切于以F、E、B、C为顶点的四边形,则⊙O的面积= ▲ .
