题目内容
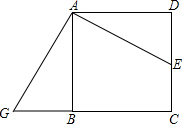如图，正方形ABCD中，边DC上有一点E，将△ADE顺时针旋转后得到△ABG，旋转中心是考点：旋转的性质,正方形的性质
专题：
分析：由△ADE旋转后能与△ABG重合，而AB=AD，∠BAD=90°，所以旋转中心是点A，旋转角为90°．
解答：解：∵△ADE旋转后能与△ABG重合．
而四边形ABCD是正方形，
∴AB=AD，∠BAD=90°，
∴旋转中心是点A，旋转角为90°．
故答案为：A，90°．
而四边形ABCD是正方形，
∴AB=AD，∠BAD=90°，
∴旋转中心是点A，旋转角为90°．
故答案为：A，90°．
点评：本题考查了旋转的性质：旋转前后的两个图形全等，对应点与旋转中心的连线段的夹角等于旋转角，对应点到旋转中心的距离相等．
练习册系列答案
阅读快车系列答案
相关题目
在Rt△ABC中，∠C=90°，AC=BC，AD是∠BAC的平分线，交BC于点D，DE⊥AB于E，若AB=10cm，则△BDE的周长等于（ ）
| A、10cm | B、8cm |
| C、12cm | D、9cm |
如图，有一块三角形的菜地ABC，∠C=90°，AC=10m，BC=24m，求菜地的另一条边AB的长．
如图，在△ABC中，点O为△ABC的内心，则∠OAC+∠OCB+∠OBA的度数为（ ）| A、45° | B、60° |
| C、90° | D、120° |
|-
|的平方根是（ ）
| 1 |
| 9 |
A、
| ||
B、
| ||
C、-
| ||
D、±
|
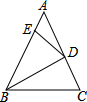如图，在△ABC中，AB=AC，∠A=44°，BD是角平分线，BE=BD，那么∠AED=