题目内容
在Rt△ABC中，∠C=90°，AC=BC，AD是∠BAC的平分线，交BC于点D，DE⊥AB于E，若AB=10cm，则△BDE的周长等于（ ）
| A、10cm | B、8cm |
| C、12cm | D、9cm |
考点：角平分线的性质,等腰直角三角形
专题：
分析：作出图形，根据角平分线上的点到角的两边的距离相等可得CD=DE，然后利用“HL”证明△ACD和△AED全等，根据全等三角形对应边相等可得AC=AE，然后求出△BDE的周长=AB．
解答：
解：如图，∵∠C=90°，AD是∠BAC的平分线，DE⊥AB，
∴CD=DE，
在△ACD和△AED中，
，
∴△ACD≌△AED（HL），
∴AC=AE，
∴△BDE的周长=BD+DE+BE=BD+CD+BE=BC+BE=AC+BE=AE+BE=AB，
∵AB=10cm，
∴△BDE的周长=10cm．
故选A．
解：如图，∵∠C=90°，AD是∠BAC的平分线，DE⊥AB，∴CD=DE，
在△ACD和△AED中，
|
∴△ACD≌△AED（HL），
∴AC=AE，
∴△BDE的周长=BD+DE+BE=BD+CD+BE=BC+BE=AC+BE=AE+BE=AB，
∵AB=10cm，
∴△BDE的周长=10cm．
故选A．
点评：本题考查了角平分线上的点到角的两边的距离相等的性质，等腰直角三角形的性质，全等三角形的判定与性质，熟记各性质是解题的关键，作出图形更形象直观．
练习册系列答案
相关题目
下列计算，结果正确的是（ ）
| A、a2•a3=a5 |
| B、（x-y）2=x2-y2 |
| C、x2y3÷2x2y=2y2 |
| D、（-3a2）3=-9a6 |
如果
+
有意义，那么x（ ）
| x-1 |
| 1-x |
| A、x≥1 | B、x≤1 |
| C、x=1 | D、不能确定 |
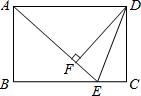如图，在矩形ABCD中，E是BC边上一点，AE=BC，DF⊥AE，垂足为F，连接DE．
加油站如何选址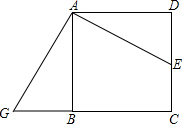
如图，正方形ABCD中，边DC上有一点E，将△ADE顺时针旋转后得到△ABG，旋转中心是