题目内容
 如图,已知△ABC是等边三角形,点D是AC边上一动点,△BDE是等边三角形,连接AE.
如图,已知△ABC是等边三角形,点D是AC边上一动点,△BDE是等边三角形,连接AE.(1)求证:△EBA≌△DBC;EA∥BC;
(2)当点D是AC边的中点,其他条件不变时,指出图中所有的垂直关系(不添加新的字母和线段).
分析:(1)由△ABC和△BDE都为等边三角形,利用等边三角形的性质得到每一个内角为60°,三边长相等,再由等式的性质得到∠ABE=∠CBD,利用SAS可得出△EBA≌△DBC,由全等三角形的对应角相等得到∠EAB=∠DCB=60°,而∠ABC=60°,得到一对内错角相等,利用内错角相等两直线平行即可得到EA与BC平行;
(2)图中所有的垂直关系为:BD⊥AC,AB⊥ED,AE⊥EB,EB⊥BC,理由分别为:当D为AC中点时,由三角形ABC为等边三角形,利用三线合一得到BD垂直于AC,BD为角平分线,得出∠ABD=30°,又∠EDB=60°,利用三角形的内角和定理及垂直的定义得到ED与AB垂直,由∠ABE=30°,∠EAB=60°,得到∠AEB为直角,可得出AE与EB垂直,由EA与BC平行,利用两直线平行同旁内角互补得到∠EBC为直角,即EB垂直于BC.
(2)图中所有的垂直关系为:BD⊥AC,AB⊥ED,AE⊥EB,EB⊥BC,理由分别为:当D为AC中点时,由三角形ABC为等边三角形,利用三线合一得到BD垂直于AC,BD为角平分线,得出∠ABD=30°,又∠EDB=60°,利用三角形的内角和定理及垂直的定义得到ED与AB垂直,由∠ABE=30°,∠EAB=60°,得到∠AEB为直角,可得出AE与EB垂直,由EA与BC平行,利用两直线平行同旁内角互补得到∠EBC为直角,即EB垂直于BC.
解答:解:(1)证明:∵△ABC和△BDE都为等边三角形,
∴∠EBD=∠ABC=∠DCB=60°,EB=DB,AB=BC,
∴∠EBD-∠ABD=∠ABC-∠ABD,即∠ABE=∠CBD,
在△EBA和△DBC中,
,
∴△EBA≌△DBC(SAS),
∴∠EAB=∠DCB=60°,又∠ABC=60°,
∴∠EAB=∠ABC,
∴EA∥BC;
(2)图中的垂直关系为:BD⊥AC,AB⊥ED,AE⊥EB,EB⊥BC.
∴∠EBD=∠ABC=∠DCB=60°,EB=DB,AB=BC,
∴∠EBD-∠ABD=∠ABC-∠ABD,即∠ABE=∠CBD,
在△EBA和△DBC中,
|
∴△EBA≌△DBC(SAS),
∴∠EAB=∠DCB=60°,又∠ABC=60°,
∴∠EAB=∠ABC,
∴EA∥BC;
(2)图中的垂直关系为:BD⊥AC,AB⊥ED,AE⊥EB,EB⊥BC.
点评:此题考查了等边三角形的性质,全等三角形的判定与性质,以及平行线的判定与性质,熟练掌握等边三角形的性质是解本题的关键.

练习册系列答案
相关题目
 的坐标为(-1,0).
的坐标为(-1,0). 如图,已知△ABC是等边三角形,AB交⊙O于点D,DE⊥AC于点E.
如图,已知△ABC是等边三角形,AB交⊙O于点D,DE⊥AC于点E.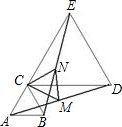 如图,已知△ABC是等边三角形,E是AC延长线上一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点,
如图,已知△ABC是等边三角形,E是AC延长线上一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点, (2012•襄城区模拟)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.
(2012•襄城区模拟)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF. (2013•奉贤区二模)如图,已知△ABC是等边三角形,点D是BC延长线上的一个动点,以AD为边作等边△ADE,过点E作BC的平行线,分别交AB,AC的延长线于点F,G,联结BE.
(2013•奉贤区二模)如图,已知△ABC是等边三角形,点D是BC延长线上的一个动点,以AD为边作等边△ADE,过点E作BC的平行线,分别交AB,AC的延长线于点F,G,联结BE.