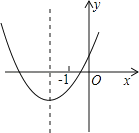题目内容
【题目】已知二次函数的图象以
为顶点，且过点
（1）求该函数的关系式；
（2）求该函数图象与坐标轴的交点坐标；
【答案】（1）
；（2）该函数的图像与坐标轴的交点是
，
，
【解析】
（1）根据图象的顶点A（1，4）来设该二次函数的关系式，然后将点B代入，即用待定系数法来求二次函数解析式；
（2）令y＝0，然后将其代入函数关系式，解一元二次方程即可，再令x=0，求出与y轴交点.
（1）由顶点A（1，4），可设二次函数关系式为y＝a（x＋1）2＋4（a≠0）．
∵二次函数的图象过点B（2，5），
∴点B（2，5）满足二次函数关系式，
∴5＝a（2＋1）2＋4，
解得a＝1．
∴二次函数的关系式是y＝（x＋1）2＋4；
（2）令x＝0，则y＝（0＋1）2＋4＝3，
∴图象与y轴的交点坐标为（0，3）；
令y＝0，则0＝（x＋1）2＋4，
解得x1＝3，x2＝1，
故图象与x轴的交点坐标是（3，0）、（1，0）．
答：图象与y轴的交点坐标为（0，3），与x轴的交点坐标是（3，0）、（1，0）．
练习册系列答案
相关题目
