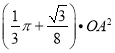Question

【题目】如图,抛物线与轴相交于,与轴相交于点,过点C作轴，交抛物线于点.

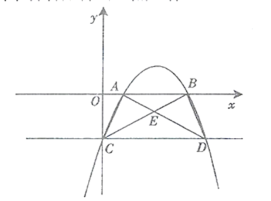
(1)求梯形ACDB的面积;

(2)若梯形ACDB的对角线交于点,求点的坐标,并求经过三点的抛物线的解析式; .

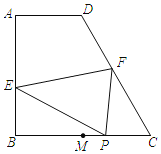
(3)点是射线上一点,且与相似,求符合条件的点坐标.

Answer 1

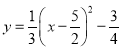【答案】(1) ；(2)；(3) ，

【解析】

（1）先求得点A、B、C、D的坐标，确定AB=3，CD=5，OC=2，再求梯形的面积即可；（2）根据对称性求得点E的横坐标，再利用平行线分线段成比例求得纵坐标，即可求过三点的抛物线的解析式；

（3）由AB∥CD得∠ABC=∠BCP，当满足，或时，与相似,即可求得点P的坐标.

（1）令中y=0，得，

解得x1=1，x2=4，

∴，

∴AB=3，

令中x=0，得y=-2，

∴，

∵轴，

∴将y=-2代入，得，

∴

∴CD=5，

∴S梯形ACDB=;

(2)由抛物线的对称性有

过，作

设过A、B、E三点的抛物线解析式为y=a（x-1）（x-4），将点E的坐标代入，得a=，

∴y=（x-1）（x-4）=

∴经过三点的抛物线的解析式为；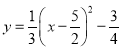

(3) 点在的右侧,

①当∠CAB=∠CPB时，

∵∥,

∴，

又∵BC=BC,

∴,

∴CP=AB=3，

∴P(3，-2)；

②当∠CAB=∠CBP时，,

∵∥,

∴,

∴△BCP∽△ABC,

∴，

∴

得，

∴，

综上，P（3,-2）或.