Question

（2013年广东梅州8分）如图，在矩形ABCD中，AB=2DA，以点A为圆心，AB为半径的圆弧交DC于点E，交AD的延长线于点F，设DA=2．

（1）求线段EC的长；

（2）求图中阴影部分的面积．

 

Answer 1

【答案】

解；（1）∵在矩形ABCD中，AB=2DA，DA=2，∴AB=AE=4。

∴。

∴。

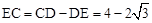（2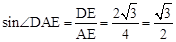）∵，∴∠DAE=60°。

∴图中阴影部分的面积为：。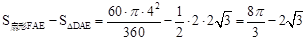

【解析】（1）根据矩形的性质得出AB=AE=4，进而利用勾股定理得出DE的长，即可得出答案。

（2）利用锐角三角函数关系得出∠DAE=60°，进而求出图中阴影部分的面积为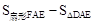：，求出即可。　

考点：矩形的性质，勾股定理，锐角三角函数定义，特殊角的三角函数值，扇形面积的计算，转换思想的应用。