题目内容
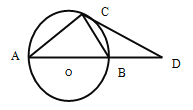
【题目】如图,直线AB和直线CD相交于点O,OF平分∠COE,过点O作OG⊥OF.

(1)若∠AOE=80°,∠COF=22°,则∠BOD= ;
(2)若∠COE=40°,试说明:OG平分∠DOE.
【答案】(1)36;(2)见解析
【解析】
(1)根据∠COF和∠AOE的度数和OF平分∠COE,求出∠AOC的度数,利用对顶角的性质得出∠BOD的人度数;
(2)根据∠COE=40°的度数求出∠EOG,再根据平角的度数求出∠AOC+∠BOG的度数之和,即∠DOG的度数,根据度数相等即可证明.
解:(1)∵∠COF=22°,OF平分∠COE,
∴∠EOF=22°,
∵∠AOE=80°,
∴∠AOC=80-22°×2=36°,
∴∠BOD=36°;
(2)∵∠COE=40°,OF平分∠COE,
∴∠COF=∠EOF=20°,
∵OG⊥OF,∴∠FOG=90°,
∴∠EOG=70°,∠COF+∠DOG=90°,
∴∠GOD=70°,
∴OG平分∠DOE.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目