题目内容
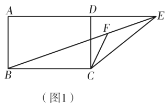
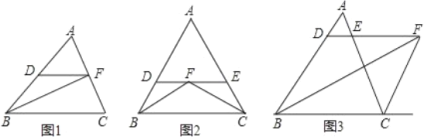
【题目】(1)如图 1,在△ABC 中,∠ABC 的平分线 BF 交 AC 于 F, 过点 F 作 DF∥BC, 求证:BD=DF.
(2)如图 2,在△ABC 中,∠ABC 的平分线 BF 与∠ACB 的平分线 CF 相交于 F,过点 F 作 DE∥BC,交直线 AB 于点 D,交直线 AC 于点 E.那么 BD,CE,DE 之间存在什么关系?并证明这种关系.
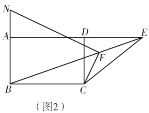
(3)如图 3,在△ABC 中,∠ABC 的平分线 BF 与∠ACB 的外角平分线 CF 相交于 F,过点 F 作 DE∥BC,交直线 AB 于点D,交直线 AC 于点 E.那么 BD,CE,DE 之间存在什么关系?请写出你的猜想.(不需证明)
【答案】(1)见详解;(2)BD+CE=DE,证明过程见详解;(3)BD﹣CE=DE,证明过程见详解
【解析】
(1)根据平行线的性质和角平分线定义得出∠DFB=∠CBF,∠ABF=∠CBF,推出∠DFB=∠DBF,根据等角对等边推出即可;
(2)与(1)证明过程类似,求出BD=DF,EF=CE,即可得出结论;
(3)与(1)证明过程类似,求出BD=DF,EF=CE,即可得出结论.
解:(1)∵BF平分∠ABC,
∴∠ABF=∠CBF,
∵DF∥BC,
∴∠DFB=∠CBF,
∴∠DFB=∠DBF,
∴BD=DF;
(2)BD+CE=DE,
理由是:∵BF平分∠ABC,
∴∠ABF=∠CBF,
∵DF∥BC,
∴∠DFB=∠CBF,
∴∠DFB=∠DBF,
∴BD=DF;
同理可证:CE=EF,
∵DE=DF+EF,
∴BD+CE=DE;
(3)BD﹣CE=DE.
理由是:∵BF平分∠ABC,
∴∠ABF=∠CBF,
∵DF∥BC,
∴∠DFB=∠CBF,
∴∠DFB=∠DBF,
∴BD=DF;
同理可证:CE=EF,
∵DE=DF﹣EF,
∴BD﹣CE=DE.