题目内容
【题目】如图,A,B两座城市相距100千米,现计划在两城市间修筑一条高速公路(即线段AB).经测量,森林保护区中心P点既在A城市的北偏东30°的方向上,又在B城市的南偏东45°的方向上.已知森林保护区的范围是以P为圆心,35千米为半径的圆形区域内.请问:计划修筑的这条高速公路会不会穿越森林保护区?请通过计算说明.(参考数据: ![]() ≈1.732,
≈1.732, ![]() ≈1.414)
≈1.414)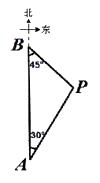
【答案】解:过P作PD⊥AB于D,
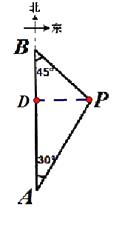
在Rt△PBD中,∠BDP=90°,∠B=45°,
∴BD=PD.
在Rt△PAD中,∠ADP=90°,∠A=30°,
∴AD= ![]() =
= ![]() =
= ![]() PD,
PD,
由题意,AD+BD=AB=100,得
![]() PD+PD=100,
PD+PD=100,
∴PD= ![]() ≈36.6>35,
≈36.6>35,
故计划修筑的高速公路不会穿过保护区.
【解析】根据在直角三角形中,三角函数定义和解直角三角形求出PD的值,得到修筑的高速公路不会穿过保护区.
【考点精析】本题主要考查了关于方向角问题的相关知识点,需要掌握指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角才能正确解答此题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目