题目内容
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰三角形CDE,其中∠DCE=90°,连接BE.
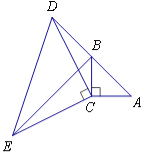
(1)求证:△ACD≌△BCE;
(2)若AB=3cm,则BE= cm;
(3)BE与AD有何位置关系?请说明理由.
【答案】(1)根据等腰直角三角形的性质可得CD=CE,由∠ACB=90°可得∠ACB=∠DCE,即可证得∠ACD=∠BCE,再结合AC=BC,即可证得结论;(2)6![]() ;(3)垂直
;(3)垂直
【解析】
试题(1)根据等腰直角三角形的性质可得CD=CE,由∠ACB=90°可得∠ACB=∠DCE,即可证得∠ACD=∠BCE,再结合AC=BC,即可证得结论;
(2)先由勾股定理求得AB=3![]() ,再由DB=AB,可得AD的长,然后根据全等三角形的性质求解即可;
,再由DB=AB,可得AD的长,然后根据全等三角形的性质求解即可;
(3)根据全等三角形的性质及三角形的面积公式求解即可
解:(1)∵△CDE是等腰直角三角形,∠DCE=90°,
∴CD=CE,
∵∠ACB=90°,
∴∠ACB=∠DCE,
∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE,
∵AC=BC
∴△ACD≌△BCE;
(2)∵AC=BC=3,∠ACB=90°,由勾股定理得:AB=3![]() ,
,
又∵DB=AB,
∴AD=2AB=6![]() ,
,
∵△ACD≌△BCE;
∴BE=AD=6![]() cm;
cm;
(3)如图所示:
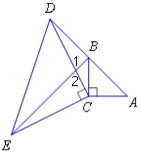
∵△ACD≌△BCE
∴∠ADC=∠BEC
∵∠1=∠2,∠DCE=90°
∴∠DBE=∠DCE=90°
∴BE⊥AD.

练习册系列答案
相关题目