题目内容
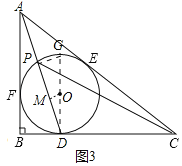
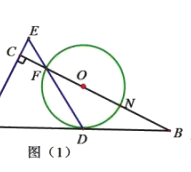
【题目】如图, Rt△ABC中,∠B=90°,它的内切圆分别与边BC、CA、AB相切于点D、E、F, (1)设AB=c, BC=a, AC=b, 求证: 内切圆半径r=![]() (a+b-c).
(a+b-c).
(2) 若AD交圆于P, PC交圆于H, FH//BC, 求∠CPD;
(3)若r=3![]() , PD=18, PC=27
, PD=18, PC=27![]() . 求△ABC各边长.
. 求△ABC各边长.
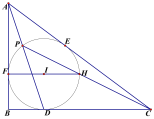
【答案】(1)证明见解析(2)45°(3)![]()
【解析】
(1)根据切线长定理,有AE=AF,BD=BF,CD=CE.易证四边形BDOF为正方形,BD=BF=r,用r表示AF、AE、CD、CE,利用AE+CE=AC为等量关系列式.
(2)∠CPD为弧DH所对的圆周角,连接OD,易得弧DH所对的圆心角∠DOH=90°,所以∠CPD=45°.
(3)由PD=18和r=3![]() 联想到垂径定理基本图形,故过圆心O作PD的垂线OM,求得弦心距OM=3,进而得到∠MOD的正切值.延长DO得直径DG,易证PG∥OM,得到同位角∠G=∠MOD.又利用圆周角定理可证∠ADB=∠G,即得到∠ADB的正切值,进而求得AB.再设CE=CD=x,用x表示BC、AC,利用勾股定理列方程即求出x.
联想到垂径定理基本图形,故过圆心O作PD的垂线OM,求得弦心距OM=3,进而得到∠MOD的正切值.延长DO得直径DG,易证PG∥OM,得到同位角∠G=∠MOD.又利用圆周角定理可证∠ADB=∠G,即得到∠ADB的正切值,进而求得AB.再设CE=CD=x,用x表示BC、AC,利用勾股定理列方程即求出x.
解:(1)证明:设圆心为O,连接OD、OE、OF,
∵⊙O分别与BC、CA、AB相切于点D、E、F
∴OD⊥BC,OE⊥AC,OF⊥AB,AE=AF,BD=BF,CD=CE
∴∠B=∠ODB=∠OFB=90°
∴四边形BDOF是矩形
∵OD=OF=r
∴矩形BDOF是正方形
∴BD=BF=r
∴AE=AF=AB-BF=c-r,CE=CD=BC-BD=a-r
∵AE+CE=AC
∴c-r+a-r=b
整理得:r=![]() (a+b-c)
(a+b-c)
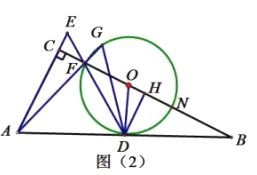
(2)取FH中点O,连接OD
∵FH∥BC
∴∠AFH=∠B=90°
∵AB与圆相切于点F,
∴FH为圆的直径,即O为圆心
∵FH∥BC
∴∠DOH=∠ODB=90°
∴∠CPD=![]() ∠DOH=45°
∠DOH=45°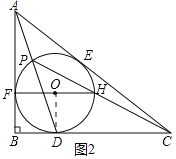
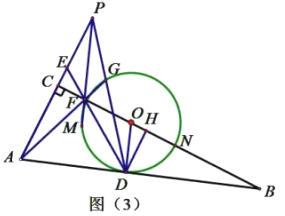
(3)设圆心为O,连接DO并延长交⊙O于点G,连接PG,过O作OM⊥PD于M
∴∠OMD=90°
∵PD=18
∴DM=![]() PD=9
PD=9
∵BF=BD=OD=r=3![]() ,
,
∴OM=![]() =
=![]() =
=![]() =3
=3
∴tan∠MOD=![]() =3
=3
∵DG为直径
∴∠DPG=90°
∴OM∥PG,∠G+∠ODM=90°
∴∠G=∠MOD
∵∠ODB=∠ADB+∠ODM=90°
∴∠ADB=∠G
∴∠ADB=∠MOD
∴tan∠ADB=![]() =tan∠MOD=3
=tan∠MOD=3
∴AB=3BD=3r=9![]()
∴AE=AF=AB-BF=9![]() 3
3![]() =6
=6![]()
设CE=CD=x,则BC=3![]() +x,AC=6
+x,AC=6![]() +x
+x
∵AB2+BC2=AC2
∴(9![]() )2.+(3
)2.+(3![]() +x)2=(6
+x)2=(6![]() +x)2
+x)2
解得:x=9![]()
∴BC=12![]() ,AC=15
,AC=15![]()
∴△ABC各边长AB=9![]() ,AC=15
,AC=15![]() ,BC=12
,BC=12![]()