Question

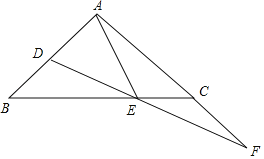
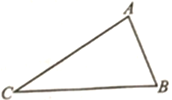
【题目】如图，△ABC中，AC=8，BC=10，AC＞AB.

(1)用尺规作图法在△ABC内求作一点D，使点D到两点A、C的距离相等，又到边AC、BC的距离相等（保留作图痕迹，不写作法）.

(2)若△ACD的周长为18，求△BCD的面积.

Answer 1

【答案】（1）见解析；（2）.

【解析】

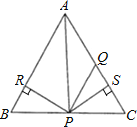
（1）分别作出∠ACB的角平分线和线段AC的垂直平分线，交点即为所求；（2）连接AD、BD，过点D作DF⊥BC于F，由垂直平分线的性质可得AD=DC，CE=AC，根据找出可得出CD的长，利用勾股定理可求出DE的长，根据角平分线的性质可得DF=DE，利用三角形面积公式即可得答案.

(1)如图所示，D点为所作

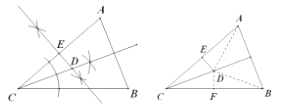
(2)连接AD、BD，过点D作DF⊥BC于F

由(1)可知AD=DC，DE垂直平分AC，即CE=AC=4，

∵，AC=8

∴CD=5，

在RtΔDEC中，.

又∵CD是∠ACB的平分线，DE⊥AC，DF⊥BC

∴DF=DE=3，

∴，