题目内容
【题目】数学课上，王老师布置如下任务：
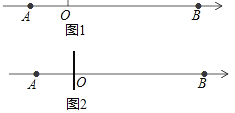
如图1，△ABC中，BC＞AB＞AC，在BC边上取一点P，使∠APC=2∠ABC．
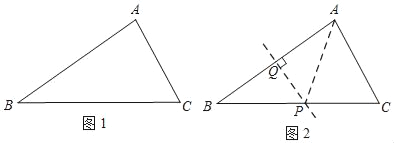
小路的作法如下，如图2：
①作AB边的垂直平分线，交BC于点P；
②连结AP．
所以，∠APC=2∠ABC．
小路的作图依据是_____．
【答案】线段垂直平分线上的点到线段两个端点的距离相等；等腰三角形两底角相等；三角形的一个外角等于于它不相邻的两个内角之和
【解析】分析：先根据线段垂直平分线的性质得：
，再由等腰三角形的性质得：
，最后利用外角的性质得：
等量代换可得结论．
详解：∵PQ是AB的垂直平分线，
∴AP=BP(线段垂直平分线上的点到线段两个端点的距离相等)，
∴∠B=∠BAP(等腰三角形两底角相等)，
∵∠APC=∠B+∠BAP(三角形的一个外角等于于它不相邻的两个内角之和)，
∴∠APC=2∠ABC，
故答案为：线段垂直平分线上的点到线段两个端点的距离相等；等腰三角形两底角相等；三角形的一个外角等于于它不相邻的两个内角之和.
练习册系列答案
相关题目
