题目内容
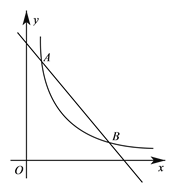
【题目】一次函数y=kx+b的图象与x、y轴分别交于点A(2,0),B(0,4).
(1)求该函数的解析式;
(2)O为坐标原点,设OA、AB的中点分别为C、D,P为OB上一动点,求PC+PD的最小值,并求取得最小值时P点的坐标.
【答案】(1)y=-2x+4;(2)2![]() ;点P的坐标为(0,1).
;点P的坐标为(0,1).
【解析】试题(1)、将A、B两点的坐标代入解析式求出k和b的值,从而得出函数解析式;(2)、首先得出点C关于y轴的对称点为C′,然后得出点D的坐标,根据C′、D的坐标求出直线C′D的解析式,从而求出点P的坐标,然后根据勾股定理得出C′D的长度,从而得出答案.
试题解析:(1)将点A、B的坐标代入y=kx+b并计算得k=-2,b=4.
∴解析式为:y=-2x+4;
(2)存在一点P,使PC+PD最小.
∵0(0,0),A(2,0),且C为AO的中点,
∴点C的坐标为(1,0), 则C关于y轴的对称点为C′(-1,0),
又∵B(0,4),A(2,0)且D为AB的中点, ∴点D的坐标为(1,2),
连接C′D,设C′D的解析式为y=kx+b,
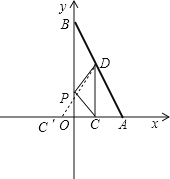
有![]() , 解得
, 解得![]() , ∴y=x+1是DC′的解析式, ∵x=0,∴y=1,
, ∴y=x+1是DC′的解析式, ∵x=0,∴y=1,
即P(0,1). ∵PC+PD的最小值=C′D,
∴由勾股定理得C′D=2![]() .
.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目