��Ŀ����
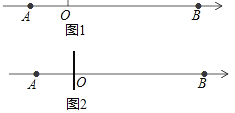
����Ŀ����ͼ1����������A���ʾ��a��B���ʾ��b��AB��ʾA���B��֮��ľ��룬��a��b����|a+4|+|b+3a|��0��
��1����A��B����֮��ľ��룻
��2�����������ϴ���һ��C����AC+BC��19����C���ʾ������
��3����ͼ2������ԭ��O����һ���壬һС��״ӵ�A����2����λ/����ٶ������˶����������һ��С���Ҵӵ�B����3����λ/����ٶ�Ҳ�����˶������������������Ĵ�С���ɿ���һ�㣩������4����λ/����ٶ����෴�����˶���������˶���ʱ��Ϊt���룩��
�ٷֱ��ʾ�ס�����С��ԭ��ľ��루�ú�t��ʽ�ӱ�ʾ����
����ס�����С��ԭ��ľ������ʱ����������λ�ö�Ӧ������
���𰸡���1��A��B����֮��ľ�����16����2����C�������߶�AB�ϣ���C��������߶�BA���ӳ����ϻ��߶�AB���ӳ����ϣ���AC+BC��19��C��ʾ����Ϊ![]() ��
��![]() ����3��������ԭ��ľ���Ϊ��12��3��t��2����������ԭ��ľ���Ϊ��2t+4���ڼס�����С��ԭ��ľ������ʱ����������λ�ö�Ӧ����Ϊ��
����3��������ԭ��ľ���Ϊ��12��3��t��2����������ԭ��ľ���Ϊ��2t+4���ڼס�����С��ԭ��ľ������ʱ����������λ�ö�Ӧ����Ϊ��![]() ��48��
��48��
��������
��1���ȸ��ݷǸ������������a��b��ֵ���ٸ��������ľ��빫ʽ�������A��B����֮��ľ��룻
��2����C�����߶�BA�ӳ����Ϻ��߶�AB�ӳ���������������ۼ�����⣻
��3���ټ���ԭ��ľ��룽�����˶���·��+OA�ij�������ԭ��ľ���������������������ӵ�B����ʼ�����˶���һֱ��ԭ��O����ʱOB�ij��ȩ������˶���·�̼�Ϊ����ԭ��ľ��룻���������ԭ��O����ʼ�����˶�����ʱ�����˶���·�̩�OB�ij��ȼ�Ϊ����ԭ��ľ��룻
�ڰ��ٷ�����������ݼס�����С��ԭ��ľ�������г�����t�ķ��̣��ⷽ�̼��ɣ�
�⣺��1����|a+4|+|b+3b|��0��
��a+4��0��b+3a��0��
��a����4��b����3a��12��
��AB��|b��a|��|12������4��|��16
��A��B����֮��ľ�����16��
��2���������ϵ�C��ʾ����Ϊc
��AC��|c��a|��|c+4|��BC��|c��b|��|c��12|
��AC+BC��19
��|c+4|+|c��12|��19
��AB��16��19
���C�������߶�AB�ϣ���C��������߶�BA���ӳ����ϻ��߶�AB���ӳ����ϣ�
�ٵ�C�����߶�BA�ӳ�����ʱ������c�ܩ�4��
��|c+4|������c+4����|c��12|������c��12��
�ੁ��c+4������c��12����19
��ã�c��![]()
�ڵ�C�����߶�AB���ӳ�����ʱ������c��12��
��|c+4|��c+4��|c��12|��c��12
��c+4+c��12��19
��ã�c��![]()
������˵����AC+BC��19��C��ʾ����Ϊ![]() ��
��![]() ��
��
��3���١����˶���·��Ϊ��2t��2t��OA��4
�������ԭ��ľ���Ϊ��2t+4
����ԭ��ľ�������������
����0��t��4ʱ������ӵ�B����ʼ�����˶���һֱ��ԭ��O��
��OB��12�������˶���·��Ϊ��3t��3t��
������ԭ��ľ���Ϊ��12��3��t��2����
����t��4ʱ�������ԭ��O����ʼһֱ�����˶���
������ԭ��ľ���Ϊ��3��t��2����12��
�ڵ�0��t��4ʱ����2t+4��12��3��t��2����
��ã�t��![]()
�ੁ4��2t��![]()
��t��4ʱ����2t+4��3��t��2����12��
��ã�t��22
�ੁ4��2t����48
�����������ס�����С��ԭ��ľ������ʱ����������λ�ö�Ӧ����Ϊ��![]() ��48��
��48��

 ����Ӣ��ϵ�д�
����Ӣ��ϵ�д�