题目内容
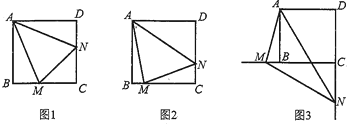
【题目】如图,已知菱形ABCD中,∠BAD=60°,点E、F分别是AB、AD上两个动点,若AE=DF,连接BF与DE相交于点G,连接CG,与BD相交于H。
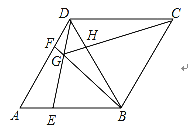
(1)求∠BGE的大小;(2)求证:GC平分∠BGD.
【答案】(1)∠BGE=60°;(2)见解析.
【解析】
(1)由题意可证△ADB是等边三角形,可得AD=AB=BD,∠DAB=∠ADB=∠ABD,由“SAS”可证△ADE≌△DBF,可得∠ADE=∠DBF,由三角形外角性质可求∠BGE的大小;
(2)过点C作CN⊥BF于点N,过点C作CM⊥ED于点M,由“AAS”可证Rt△CBN≌Rt△CDM,可得CM=CN,由角平分线的性质可得结论.
(1)∵ABCD为菱形,
∴AB=AD.
∵∠BAD=60°,
∴△ABD为等边三角形.
∴∠A=∠BDF=60°.
又∵AE=DF,AD=BD,
∴△AED≌△DFB;
∴∠DBG=∠ADE
∴∠EGB=∠DBG+∠BDG=∠ADE+∠BDG=∠ADB=60°
(2)如图,过点C作CN⊥BF于点N,过点C作CM⊥ED于点M,

由(1)得∠ADE=∠DBF
∴∠CBF=60°+∠DBF
=60°+∠ADE
=∠DEB
又∠DEB=∠MDC
∴∠CBF=∠CDM
∵BC=CD,∠CBF=∠CDM,∠CMD=∠CNG=90°
∴Rt△CBN≌Rt△CDM(AAS)
∴CN=CM,且CN⊥BF,CM⊥ED
∴点C在∠BGD的平分线上
即GC平分∠BGD.

练习册系列答案
相关题目