题目内容
【题目】完成下列填空:
已知:如图,AB∥CD,∠B=120°,CA平分∠BCD.求证:∠1=30°.
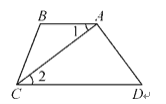
证明:∵AB∥CD( ),
∴∠B+∠BCD= ( ).
∵∠B= ( ),
∴∠BCD= ( ).
又∵CA平分∠BCD( ),
∴∠2= ( ).
∵AB∥CD( ),
∴∠1= =30°( ).
【答案】见解析.
【解析】由条件AB∥CD,根据“两直线平行,内错角相等”可得到∠1=∠2,因此求∠1的度数可转化为求∠2的度数,而CA平分∠BCD,则应求∠BCD的度数.由图知∠BCD与已知的∠B是直线AB、CD被直线BC所截得的同旁内角,由条件AB∥CD可知它们互补.
∵AB∥CD(__已知__),
∴∠B+∠BCD=__180_°__(__两直线平行,同旁内角互补__).
∵∠B=__120_°__(__已知__),
∴∠BCD=__60_°__(__等式的性质__).
又∵CA平分∠BCD(__已知__),
∴∠2=__30_°__(__角平分线定义__).
∵AB∥CD(__已知__),
∴∠1=__∠2__=30°(__两直线平行,内错角相等__).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目