题目内容
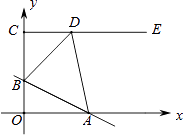
【题目】如图，有两根直杆隔河相对，杆CD高30m，杆AB高20m，两杆相距50m.现两杆上各有一只鱼鹰，它们同时看到两杆之间的河面上E处浮起一条小鱼，于是以同样的速度同时飞下来夺鱼，结果两只鱼鹰同时到达，叼住小鱼．问两杆底部距鱼的距离各是多少？
【答案】两杆杆底到E处的水平距离分别是30m和20m.
【解析】根据题意结合勾股定理得出AB2+BE2=EC2+DC2，进而得出答案．
由题意可得AE＝DE.在Rt△ABE和Rt△DEC中，
由勾股定理得AE2＝AB2＋BE2，DE2＝EC2＋CD2，
∴AB2＋BE2＝EC2＋CD2，即202＋BE2＝(50－BE)2＋302，
解得BE＝30m，
则EC＝50－30＝20(m)．
答：两杆杆底到E处的水平距离分别是30m和20m.
练习册系列答案
相关题目
【题目】某学校计划在总费用2300元的限额内，租用客车送234名学生和6名教师集体外出活动，每辆客车上至少要有1名教师.现有甲、乙两种大客车，它们的载客量和租金如下表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 45 | 30 |
租金/(元/辆) | 400 | 280 |
(1)共需租多少辆客车?
(2)请给出最节省费用的租车方案.
