��Ŀ����
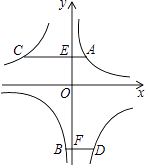
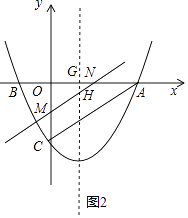
����Ŀ����ͼ��������y=ax2+bx��2��x�ύ��A��B���㣬��y�ύ��C�㣬��֪A��3��0������M��1���� ![]() ��������������һ�㣮
��������������һ�㣮
��1����a��b��ֵ��
��2������AC�����P��y������һ�㣬����P��A��C����Ϊ������������ǵ��������Σ���P������ꣻ
��3������N��x���������������������ڵ�һ���㣨����O��A�غϣ�������N��NH��AC�������ߵĶԳ�����H�㣮��ON=t����ONH�����ΪS����S��t֮��ĺ�����ϵʽ��
���𰸡�
��1��
�⣺��A��3��0������M��1���� ![]() ������y=ax2+bx��2��
������y=ax2+bx��2�� 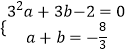 ��
��
��ã� 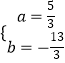
��2��
�⣺��y=ax2+bx��2�У���x=0ʱ��y=��2��
��C��0����2����
��OC=2��
��ͼ����P��0��m������PC=m+2��OA=3��AC= ![]() =
= ![]() ��
��
�ٵ�PA=CAʱ����OP1=OC=2��
��P1��0��2����
�ڵ�PC=CA= ![]() ʱ����m+2=
ʱ����m+2= ![]() ����m=
����m= ![]() ��2��
��2��
��P2��0�� ![]() ��2����
��2����
�۵�PC=PAʱ����P��AC�Ĵ�ֱƽ�����ϣ�
���AOC�ס�P3EC��
�� ![]() =
= ![]() ��
��
��P3C= ![]() ��
��
��m= ![]() ��
��
��P3��0�� ![]() ����
����
�ܵ�PC=CA= ![]() ʱ��m=��2��
ʱ��m=��2�� ![]() ��
��
��P4��0����2�� ![]() ����
����
����������P�������1��0��2����0�� ![]() ��2����0��
��2����0�� ![]() ����0����2��
����0����2�� ![]() ��
��
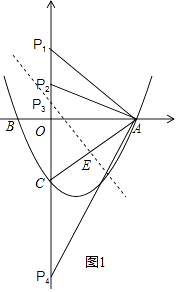
��3��
�⣺��H��HG��OA��G����HN��Y����M��
��NH��AC��
�� ![]() ��
��
�� ![]() ��
��
��OM= ![]() ��
��
�������ߵĶԳ���Ϊֱ��x= ![]() =
= ![]() ��
��
��OG= ![]() ��
��
��GN=t�� ![]() ��
��
��GH��OC��
���NGH�ס�NOM��
�� ![]() ��
��
�� ![]() =
= ![]() ��
��
��HG= ![]() t��
t�� ![]() ��
��
��S= ![]() ONGH=
ONGH= ![]() t��
t�� ![]() t��
t�� ![]() ��=
��= ![]() t2��
t2�� ![]() t��0��t��3����
t��0��t��3����
����������1�����������з����鼴�ɵõ����ۣ���2����y=ax2+bx��2�У���x=0ʱ��y=��2���õ�OC=2����ͼ����P��0��m������PC=m+2��OA=3�����ݹ��ɶ����õ�AC= ![]() =
= ![]() ���ٵ�PA=CAʱ����OP1=OC=2���ڵ�PC=CA=
���ٵ�PA=CAʱ����OP1=OC=2���ڵ�PC=CA= ![]() ʱ���۵�PC=PAʱ����P��AC�Ĵ�ֱƽ�����ϣ��������������ε����ʵõ�P3��0��
ʱ���۵�PC=PAʱ����P��AC�Ĵ�ֱƽ�����ϣ��������������ε����ʵõ�P3��0�� ![]() �����ܵ�PC=CA=
�����ܵ�PC=CA= ![]() ʱ�����ǵõ����ۣ���3����H��HG��OA��G����HN��Y����M������ƽ���߷��߶γɱ��������õ�OM=
ʱ�����ǵõ����ۣ���3����H��HG��OA��G����HN��Y����M������ƽ���߷��߶γɱ��������õ�OM= ![]() ����������ߵĶԳ���Ϊֱ��x=
����������ߵĶԳ���Ϊֱ��x= ![]() =
= ![]() ���õ�OG=
���õ�OG= ![]() �����GN=t��
�����GN=t�� ![]() ���������������ε����ʵõ�HG=
���������������ε����ʵõ�HG= ![]() t��
t�� ![]() �����ǵõ����ۣ�
�����ǵõ����ۣ�
�����㾫����������Ŀ����֪���������ù��ɶ����ĸ����ƽ���߷��߶γɱ��������֪ʶ���Եõ�����Ĵ𰸣���Ҫ����ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2������ƽ���߽�����ֱ�ߣ����õĶ�Ӧ�߶γɱ�����

 ֥�鿪���γ�������ϵ�д�
֥�鿪���γ�������ϵ�д�