Question

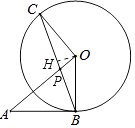
【题目】如图，AB与⊙O相切于点B，BC为⊙O的弦，OC⊥OA，OA与BC相交于点P．
（1）求证：AP=AB；
（2）若OB=4，AB=3，求线段BP的长．

Answer 1

【答案】
（1）证明：∵OC=OB，

∴∠OCB=∠OBC，

∴AB是⊙O的切线，

∴OB⊥AB，

∴∠OBA=90°，

∴∠ABP+∠OBC=90°，

∵OC⊥AO，

∴∠AOC=90°，

∴∠OCB+∠CPO=90°，

∵∠APB=∠CPO，

∴∠APB=∠ABP，

∴AP=AB

（2）解：作OH⊥BC于H．

在Rt△OAB中，∵OB=4，AB=3，

∴OA= =5，

∵AP=AB=3，

∴PO=2．

在Rt△POC中，PC= =2 ，

∵ PCOH= OCOP，

∴OH= = ，

∴CH= = ，

∵OH⊥BC，

∴CH=BH，

∴BC=2CH= ，

∴PB=BC﹣PC= ﹣2 = ．

【解析】（1）欲证明AP=AB，只要证明∠APB=∠ABP即可；（2）作OH⊥BC于H．在Rt△POC中，求出OP、PC、OH、CH即可解决问题．
【考点精析】利用切线的性质定理对题目进行判断即可得到答案，需要熟知切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径．