题目内容
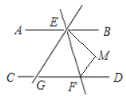
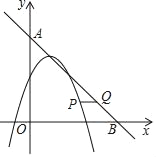
【题目】在等边三角形ABC中，点D是BC的中点，点E、F分别是边AB、AC（含线段AB、AC的端点）上的动点，且∠EDF=120°，小明和小慧对这个图形展开如下研究：
问题初探：
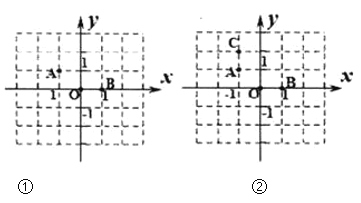
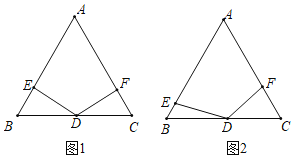
（1）如图1，小明发现：当∠DEB=90°时，BE+CF=nAB，则n的值为______；
问题再探：
（2）如图2，在点E、F的运动过程中，小慧发现两个有趣的结论：
①DE始终等于DF；②BE与CF的和始终不变；请你选择其中一个结论加以证明．
成果运用
（3）若边长AB=4，在点E、F的运动过程中，记四边形DEAF的周长为L，L=DE+EA+AF+FD，则周长L的变化范围是______．
【答案】（1）
；（2）BE与CF的和始终不变，见解析；（3）
【解析】
（1）先利用等边三角形判断出BD=CD=AB，进而判断出BE=BD，再判断出∠DFC=90°，得出CF=CD，即可得出结论；
（2）①构造出△EDG≌△FDH（ASA），得出DE=DF，即可得出结论；
②由（1）知，BG+CH=AB，由①知，△EDG≌△FDH（ASA），得出EG=FH，即可得出结论；
（3）由（1）（2）判断出L=2DE+6，再判断出DE⊥AB时，L最小，点F和点C重合时，DE最大，即可得出结论．
解：（1）∵△ABC是等边三角形，
∴∠B=∠C=60°，AB=BC，
∵点D是BC的中点，
∴BD=CD=BC=AB，
∵∠DEB=90°，
∴∠BDE=90°-∠B=30°，
在Rt△BDE中，BE=BD，
∵∠EDF=120°，∠BDE=30°，
∴∠CDF=180°-∠BDE-∠EDF=30°，
∵∠C=60°，
∴∠DFC=90°，
在Rt△CFD中，CF=CD，
∴BE+CF=BD+CD=BC=AB，
∵BE+CF=nAB，
∴n=，
故答案为；
（2）如图2
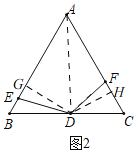
①过点D作DG⊥AB于G，DH⊥AC于H，
∴∠DGB=∠AGD=∠CFD=∠AHF=90°，
∵△ABC是等边三角形，
∴∠A=60°，
∴∠GDH=360°-∠AGD-∠AHD-∠A=120°，
∵∠EDF=120°，
∴∠EDG=∠FDH，
∵△ABC是等边三角形，且D是BC的中点，
∴∠BAD=∠CAD，
∵DG⊥AB，DH⊥AC，
∴DG=DH，
在△EDG和△FDH中，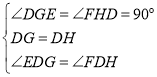
，
∴△EDG≌△FDH（ASA），
∴DE=DF，
即：DE始终等于DF；
②同（1）的方法得，BG+CH=AB，
由①知，△EDG≌△FDH（ASA），
∴EG=FH，
∴BE+CF=BG-EG+CH+FH=BG+CH=AB，
∴BE与CF的和始终不变
（3）由（2）知，DE=DF，BE+CF=AB，
∵AB=4，
∴BE+CF=2，
∴四边形DEAF的周长为L=DE+EA+AF+FD
=DE+AB-BE+AC-CF+DF
=DE+AB-BE+AB+DE
=2DE+2AB-（BE+CF）
=2DE+2×4-2
=2DE+6，
∴DE最大时，L最大，DE最小时，L最小，
当DE⊥AB时，DE最小，
由（1）知，BG=BD=1，
∴DE最小=
BG=，
∴L最小=2+6，
当点F和点C重合时，DE最大，此时，∠BDE=180°-∠EDF=120°=60°，
∵∠B=60°，
∴∠B=∠BDE=∠BED=60°，
∴△BDE是等边三角形，
∴DE=BD=AB=2，
即：L最大=2×2+6=10，
∴周长L的变化范围是2≤L≤10，
故答案为2≤L≤10．
