题目内容
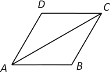
【题目】如图,在□ABCD中,点E、F分别在边AB、DC上,下列条件不能使四边形EBFD是平行四边形的条件是( )

A.DE=BFB.AE=CFC.DE∥FBD.∠ADE=∠CBF
【答案】A
【解析】
根据平行四边形的性质可得AB∥CD,添加DE=BF后,满足一组对边平行,另一组对边相等,不符合平行四边形的判定方法,进而可判断A项;
根据平行四边形的性质可得AB∥CD,AB=CD,进一步即得BE=DF,根据一组对边平行且相等的四边形是平行四边形即可判断B项;
根据平行四边形的性质可得AB∥CD,进而根据平行四边形的定义可判断C项;
根据平行四边形的性质可证明△ADE≌△CBF,进而可得AE=CF,DE=BF,然后根据两组对边相等的四边形是平行四边形即可判断D项.
解:A、∵四边形ABCD是平行四边形,∴AB∥CD,由DE=BF,不能判定四边形EBFD是平行四边形,所以本选项符合题意;
B、∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,
∵AE=CF,∴BE=DF,∴四边形EBFD是平行四边形,所以本选项不符合题意;
C、∵四边形ABCD是平行四边形,∴AB∥CD,
∵DE∥FB,∴四边形EBFD是平行四边形,所以本选项不符合题意;
D、∵四边形ABCD是平行四边形,∴∠A=∠C,AD=CB,AB=CD,
∵∠ADE=∠CBF,∴△ADE≌△CBF(ASA),∴AE=CF,DE=BF,
∴BE=DF,∴四边形EBFD是平行四边形,所以本选项不符合题意.
故选:A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目