题目内容
【题目】如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)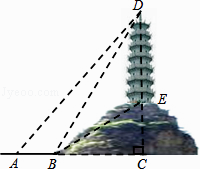
【答案】解:由题知,∠DBC=60°,∠EBC=30°,
∴∠DBE=∠DBC﹣∠EBC=60°﹣30°=30°.
又∵∠BCD=90°,
∴∠BDC=90°﹣∠DBC=90°﹣60°=30°.
∴∠DBE=∠BDE.
∴BE=DE.
设EC=x,则DE=BE=2EC=2x,DC=EC+DE=x+2x=3x,
BC= ![]() =
= ![]() =
= ![]() x,
x,
由题知,∠DAC=45°,∠DCA=90°,AB=20,
∴△ACD为等腰直角三角形,
∴AC=DC.
∴ ![]() x+60=3x,
x+60=3x,
解得:x=30+10 ![]() .
.
答:塔高约为30+10 ![]() m.
m.
【解析】先求出∠DBE=30°,∠BDE=30°,得出BE=DE,然后设EC=x,则BE=2x,DE=2x,DC=3x,BC= ![]() x,然后根据∠DAC=45°,可得AC=CD,列出方程求出x的值,然后即可求出塔DE的高度.
x,然后根据∠DAC=45°,可得AC=CD,列出方程求出x的值,然后即可求出塔DE的高度.
【考点精析】本题主要考查了关于仰角俯角问题的相关知识点,需要掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目








