��Ŀ����
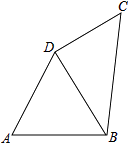
����Ŀ��ijУ��ѧ��ȤС�鿪չ��һ�ο������������£���ͼ�٣�������ABCD�У�AB=4�������ǰ����������ABCD�ϣ�ʹ���ǰ��ֱ�Ƕ�����D���غϣ����ǰ��һ�߽�AB�ڵ�P����һ�߽�BC���ӳ����ڵ�Q�� 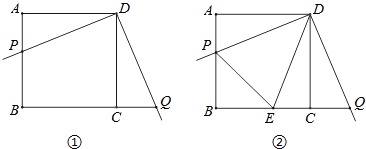
��1����֤��AP=CQ��
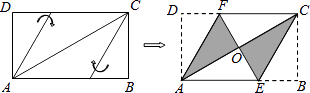
��2����ͼ�ڣ�С����ͼ1�Ļ���������PDQ��ƽ����DE��BC�ڵ�E������PE��������PE��QE����һ����������ϵ����²����Ľ��۲�����֤����
��3���ڣ�2���������£���AP=1����PE�ij���
���𰸡�
��1��֤�������ı���ABCD�������Σ�
���ADC=��A=��B=��BCD=��DCQ=90�㣬AD=BC=CD=AB=4��
�ߡ�PDQ=90�㣬
���ADP=��CDQ��
�ڡ�APD�͡�CQD�У�
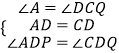 ��
��
���APD�ա�CQD��ASA����
��AP=CQ
��2���⣻PE=QE���������£�
�ɣ�1���ã���APD�ա�CQD��
��PD=QD��
��DEƽ�֡�PDQ��
���PDE=��QDE��
�ڡ�PDE�͡�QDE�У�
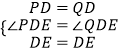 ��
��
���PDE�ա�QDE��SAS����
��PE=QE
��3���⣺�ɣ�2���ã�PE=QE���ɣ�1���ã�CQ=AP=1��
��BQ=BC+CQ=5��BP=AB��AP=3��
��PE=QE=x����BE=5��x��
��Rt��BPE�У��ɹ��ɶ����ã�32+��5��x��2=x2��
��ã�x=3.4��
��PE�ij�Ϊ3.4
����������1���������ε����ʵó���ADC=��A=��B=��BCD=��DCQ=90�㣬AD=BC=CD=AB=4��֤����ADP=��CDQ����ASA֤����APD�ա�CQD���ó���Ӧ����ȼ��ɣ���2����ȫ�������ε����ʵó�PD=QD��֤����PDE=��QDE����SAS֤����PDE�ա�QDE���ó���Ӧ����ȼ��ɣ���3���ɣ�2���ͣ�1���ó�PE=QE��CQ=AP=1�����BQ=BC+CQ=5��BP=AB��AP=3����PE=QE=x����BE=5��x����Rt��BPE�У��ɹ��ɶ����ó����̣��ⷽ�̼��ɣ�
�����㾫����������Ҫ�����������ε����ʵ����֪ʶ�㣬��Ҫ�����������ĸ��Ƕ���ֱ�ǣ������߶���ȣ������ε������Խ�����ȣ����һ��ഹֱƽ�֣�ÿ���Խ���ƽ��һ��Խǣ������ε�һ���Խ��߰������ηֳ�����ȫ�ȵĵ���ֱ�������Σ������εĶԽ�����ߵļн���45o�������ε������Խ��߰���������ηֳ��ĸ�ȫ�ȵĵ���ֱ�������β�����ȷ�����⣮