Question

【题目】赛龙舟是端午节的主要习俗，某市甲乙两支龙舟队在端午节期间进行划龙舟比赛，从起点A驶向终点B，在整个行程中，龙舟离开起点的距离y（米）与时间x（分钟）的对应关系如图所示，请结合图象解答下列问题：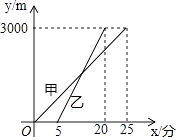

（1）起点A与终点B之间相距多远？
（2）哪支龙舟队先出发？哪支龙舟队先到达终点？
（3）分别求甲、乙两支龙舟队的y与x函数关系式；
（4）甲龙舟队出发多长时间时两支龙舟队相距200米？

Answer 1

【答案】
（1）解：由图可得，起点A与终点B之间相距3000米；
（2）解：由图可得，甲龙舟队先出发，乙龙舟队先到达终点；
（3）解：设甲龙舟队的y与x函数关系式为y=kx，

把（25，3000）代入，可得3000=25k，

解得k=120，

∴甲龙舟队的y与x函数关系式为y=120x（0≤x≤25），

设乙龙舟队的y与x函数关系式为y=ax+b，

把（5，0），（20，3000）代入，可得

，

解得 ，

∴乙龙舟队的y与x函数关系式为y=200x﹣1000（5≤x≤20）；

（4）解：令120x=200x﹣1000，可得x=12.5，

即当x=12.5时，两龙舟队相遇，

当x＜5时，令120x=200，则x= （符合题意）；

当5≤x＜12.5时，令120x﹣（200x﹣1000）=200，则x=10（符合题意）；

当12.5＜x≤20时，令200x﹣1000﹣120x=200，则x=15（符合题意）；

当20＜x≤25时，令3000﹣120x=200，则x= （符合题意）；

综上所述，甲龙舟队出发 或10或15或 分钟时，两支龙舟队相距200米

【解析】（1）由已知条件利用函数图象即可求出两点距离；
（2）根据函数图象即可得出所求结论；
（3）先设甲龙舟队的y与x函数关系式为y=kx，把（25，3000）代入，可得甲龙舟队的y与x函数关系式；再设乙龙舟队的y与x函数关系式为y=ax+b，把（5，0），（20，3000）代入，可得乙龙舟队的y与x函数关系式；
（4）根据题意分四种情况进行讨论，由已知条件分别列方程求解即可得到结论．