题目内容
【题目】数学活动问题情境:
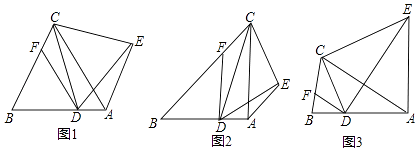
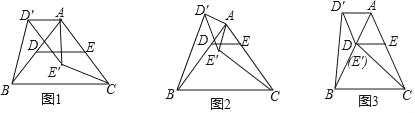
如图1,在△ABC中,AB=AC,∠BAC=90°,D,E分别是边AB,AC的中点,将△ADE绕点A顺时针旋转α角(0°<α<90°)得到△AD′E′,连接CE′,BD′.探究CE′与BD′的数量关系;
探究发展:
(1)图1中,猜想CE′与BD′的数量关系,并证明;
(2)如图2,若将问题中的条件“D,E分别是边AB,AC的中点”改为“D为AB边上任意一点,DE∥BC交AC于点E“,其他条件不变,(1)中CE′与BD′的数量关系还成立吗?请说明理由;
拓展延伸:
(3)如图3,在△ABC中,AB=AC,∠BAC=60°,点D,E分别在AB,AC上,且DE∥BC,将△ADE绕点A顺时针旋转60°得到△AD′E′,连接CE′,BD′,请你仔细观察,提出一个你最关心的数学问题(例如:CE′与BD′相等吗?).
【答案】解:(1)CE′=BD′;(2)结论不变;(3)结论:①△D′AB≌△E′AC,②△D′DB≌△DEC,③∠BD′D=∠CDE,④四边形AD′DE是菱形.(答案不唯一)
【解析】
(1)如图1中,结论:CE′=BD′.只要证明△D′AB≌△E′AC即可;
(2)结论不变,证明方法类似;
(3)结论:①△D′AB≌△E′AC,②△D′DB≌△DEC,③∠BD′D=∠CDE,④四边形AD′DE是菱形.(答案不唯一)
解:(1)如图1中,结论:CE′=BD′.
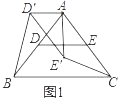
理由:∵AB=AC,AD=DB,AE=EC,
∴AD=AE,AD′=AE′,∠D′AE′=∠BAC=90°,
∴∠D′AB=∠E′AC,
在△D′AB和△′AC中,
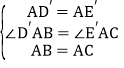 ,
,
∴△D′AB≌△E′AC,
∴BD′=CE′.
(2)如图2中,结论不变.
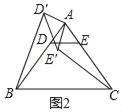
理由:∵AB=AC,
∴∠ABC=∠ACB,
∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB,
∴∠ADE=∠AED,
∴AD=AE,AD′=AE′,∠D′AE′=∠BAC=90°,
∴∠D′AB=∠E′AC,
在△D′AB和△′AC中,
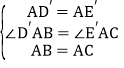 ,
,
∴△D′AB≌△E′AC,
∴BD′=CE′.
(3)如图3中,结论:①△D′AB≌△E′AC,②△D′DB≌△DEC,③∠BD′D=∠CDE,④四边形AD′DE是菱形.(答案不唯一)
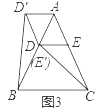
理由:∵△ADE,△AD′D,△ABC都是等边三角形,
∴D′A=AD,∥D′AB=∠DAC=60°,AB=AC,
∴△D′AB≌△DAC.
由DD′=DE,∠D′DB=∠DEC=120°.BD=EC,
可得△D′DB≌△DEC,
∴∠BD′D=∠CDE,
∵AD′=DD′=DE=AE,
∴四边形AD′DE是菱形.