题目内容
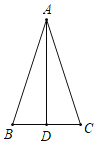
【题目】如图,在△ABC中,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA.
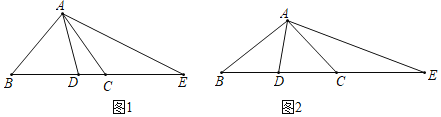
(1)若∠BAC=90°(图1),求∠DAE的度数;
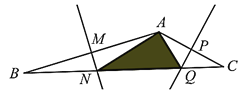
(2)若∠BAC=120°(图2),求∠DAE的度数;
(3)当∠BAC>90°时,探求∠DAE与∠BAC之间的数量关系,直接写出结果.
【答案】(1)∠DAE=45°,(2)∠DAE=60°;(3)∠DAE=![]() ∠BAC
∠BAC
【解析】
(1)由于AB=AC,∠BAC=90°,从而求出∠B=∠ACB=45°,又因为BD=BA,可知∠BAD=∠BDA=67.5°,因为CE=CA,可知∠CAE=∠E=![]() ∠ACB=22.5°,最后可求出得∠DAE=∠BAE﹣∠BAD=45°.
∠ACB=22.5°,最后可求出得∠DAE=∠BAE﹣∠BAD=45°.
(2)由于AB=AC,∠BAC=120°,从而求出∠B=∠ACB=30°,又因为BD=BA,可知∠BAD=∠BDA=75°,因为CE=CA,可知∠CAE=∠E=![]() ∠ACB=15°,最后可求出得∠DAE=∠BAE﹣∠BAD=60°.
∠ACB=15°,最后可求出得∠DAE=∠BAE﹣∠BAD=60°.
(3)可设∠CAE=x,∠BAD=y,则∠B=180°﹣2y,∠E=∠CAE=x,从而可知∠BAE=2y﹣x,∠DAE=y﹣x,∠BAC=2y﹣2x,所以可知∠DAE=![]() ∠BAC,
∠BAC,
(1)如图1,∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵BD=BA,
∴∠BAD=∠BDA=![]() (180°﹣∠B)=67.5°,
(180°﹣∠B)=67.5°,
∵CE=CA
∴∠CAE=∠E=![]() ∠ACB=22.5°,
∠ACB=22.5°,
∴∠BAE=180°﹣∠B﹣∠E=112.5°,
∴∠DAE=∠BAE﹣∠BAD=45°,
(2)如图2,∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=30°,
∵BA=BD,
∴∠BAD=∠BDA=75°,
∴∠DAC=45°,
∵CA=CE,
∴∠E=∠CAE=15°,
∴∠DAE=∠DAC+∠CAE=60°;
(3)∠DAE=![]() ∠BAC,
∠BAC,
理由:设∠CAE=x,∠BAD=y,
则∠B=180°﹣2y,∠E=∠CAE=x,
∴∠BAE=180°﹣∠B﹣∠E=2y﹣x,
∴∠DAE=∠BAE﹣∠BAD=2y﹣x﹣y=y﹣x,
∠BAC=∠BAE﹣∠CAE=2y﹣x﹣x=2y﹣2x
∴∠DAE=![]() ∠BAC.
∠BAC.

 备战中考寒假系列答案
备战中考寒假系列答案