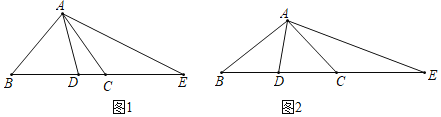题目内容
【题目】已知直线m∥n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P为线段CD的中点.
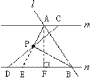
(1)操作发现:直线l⊥m,分别交m、n于点A、B,当点B与点D重合时(如图1),连结PA,请直接写出线段PA与PB的数量关系: .
(2)猜想证明:在图1的情况下,把直线l向右平移到如图2的位置,试问(1)中的PA与PB
的关系式是否仍然成立?若成立,请给予证明;若不成立,请说明理由.
(3)延伸探究:在图2的情况下,把直线l绕点A旋转,使得∠APB=90°(如图3),若两平行线m、n之间的距离为2k,求证:PAPB=kAB.

【答案】(1)PA=PB;(2)![]() 成立,证明详见解析;(3)详见解析.
成立,证明详见解析;(3)详见解析.
【解析】
(1)根据△CBD是直角三角形,而且点P为线段CD的中点,应用直角三角形的性质,可得PA=PB,据此解答即可.
(2)PA=PB仍然成立.如图,延长AP交直线n于点E.只要证明PA=PE即可;
(3)延长AP交直线n于点E,作AF⊥直线n于点F.只要证明△AEF∽△BEP,可得![]() ,推出AEBP=AFBE,由AF=2k,AE=2PA,BE=AB,推出2PAPB=2kAB,可得PAPB=AB.
,推出AEBP=AFBE,由AF=2k,AE=2PA,BE=AB,推出2PAPB=2kAB,可得PAPB=AB.
解:![]() .
.
![]() 成立.如图,延长AP交直线m于点E.
成立.如图,延长AP交直线m于点E.
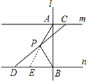
![]() m
m![]() n,
n,
![]() ,
,![]() ,
,
又![]() ,
,
![]() ≌
≌![]() .
.
![]() ,即点P是AE的中点,
,即点P是AE的中点,
又![]() ,
,
![]() 直角三角形斜边上的中线等于斜边的一半
直角三角形斜边上的中线等于斜边的一半![]() .
.
![]() 如图,延长AP交直线n于点E,作
如图,延长AP交直线n于点E,作![]() 直线n于点
直线n于点![]()
由![]() 得
得![]() ,
,
又![]() ,
,
![]() 是线段AE的垂直平分,
是线段AE的垂直平分,
![]()
![]() ,
,![]() ,
,
![]() ∽
∽![]() .
.
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() .
.

练习册系列答案
相关题目