Question

【题目】如图，AD是△ABC的中线，AB：AD：BC＝13：12：10，△ABD的周长是60cm．求AC．

Answer 1

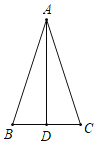
【答案】AC＝26（cm）

【解析】

设AB＝13x，AD＝12x，BC＝10x，则BD＝CD＝5x，所以13x+12x+5x＝60，解得x＝2，根据勾股定理的逆定理可证明△ABD为直角三角形，∠ADB＝90°，所以AD垂直平分BC，从而得出答案即可.

设AB＝13x，AD＝12x，BC＝10x，

∵AD是△ABC的中线，

∴BD＝CD＝5x，

∵△ABD的周长是60cm，

∴13x+12x+5x＝60，解得x＝2，

∴BD＝10，AD＝24，AB＝26，

∵102+242＝262，

∴BD2+AD2＝AB2，

∴△ABD为直角三角形，∠ADB＝90°，

∴AD⊥BC，

而BD＝CD，

∴AC＝AB＝26（cm）．