题目内容
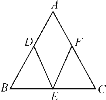
【题目】如图,△ABC中,AB=AC,点D,E,F分别是△ABC边AB,BC,AC的中点,连接DE,EF,要使四边形ADEF是正方形,还需增加条件:_______.
【答案】∠A=90°
【解析】
由已知点D、E、F分别是△ABC的边AB、BC、AC的中点,并且AB=AC,从而得到四边形ADEF是菱形,由一角为直角的菱形为正方形.故需要添加∠A=90°.
∵点D、E、F分别是△ABC的边AB、BC、AC的中点,
∴EF=AD=BD=![]() AB, DE=AF=CFD=
AB, DE=AF=CFD=![]() AC,
AC,
∵AB=AC,
∴AD=DE=EF=AF,
∴四边形ADEF是菱形.
如果有一角为直角,菱形就成为正方形.故添加∠A=90°即可.
故答案为:∠A=90°(此题答案不唯一).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某商店分两次购进![]() 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量(件) | 购进所需费用(元) | ||
|
| ||
第一次 | 30 | 40 | 3800 |
第二次 | 40 | 30 | 3200 |
(1) 求![]() 两种商品每件的进价分别是多少元?
两种商品每件的进价分别是多少元?
(2) 商场决定![]() 种商品以每件30元出售,
种商品以每件30元出售,![]() 种商品以每件100元出售.为满足市场需求,需购进
种商品以每件100元出售.为满足市场需求,需购进![]() 两种商品共1000件,且
两种商品共1000件,且![]() 种商品的数量不少于
种商品的数量不少于![]() 种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.