ЬтФПФкШн
ЁОЬтФПЁПРрБШЬиЪтЫФБпаЮЕФбЇЯАЃЌЮвУЧПЩвдЖЈвхЃКгавЛзщЖдНЧЯрЕШЖјСэвЛзщЖдНЧВЛЯрЕШЕФЭЙЫФБпаЮНазіЁАЕШЖдНЧЫФБпаЮЁБЃЎ
ЬНЫїЬхбщ
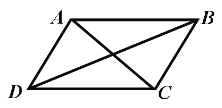
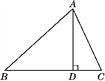
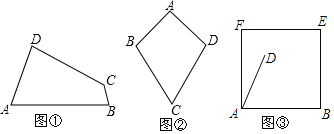
ЃЈ1ЃЉШчЭМЂйЃЌвбжЊЫФБпаЮABCDЪЧЁАЕШЖдНЧЫФБпаЮЁБЃЌЁЯAЁйЁЯCЃЌЁЯA=70ЁуЃЌЁЯB=80ЁуЃЎЧѓЁЯCЃЌЁЯDЕФЖШЪ§ЃЎ
ЃЈ2ЃЉШчЭМЂкЃЌШєAB=AD=aЃЌCB=CD=bЃЌЧвaЁйbЃЌФЧУДЫФБпаЮABCDЪЧЁАЕШЖдНЧЫФБпаЮЁБТ№ЃПЪдЫЕУїРэгЩЃЎ
ГЂЪдгІгУ
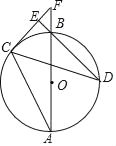
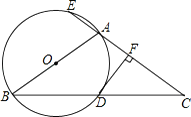
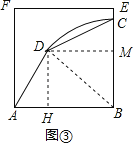
ЃЈ3ЃЉШчЭМЂлЃЌдкБпГЄЮЊ6ЕФе§ЗНаЮФОАхABEFЩЯВУГіЁАЕШЖдНЧЫФБпаЮЁБABCDЃЌШєвбОШЗЖЈDA=4ЃЌЁЯDAB=60ЁуЃЌЪЧЗёдке§ЗНаЮABEFФкЃЈАќРЈБпЩЯЃЉДцдквЛЕуЕуCЃЌЪЙЫФБпаЮABCDвдЁЯDAB=ЁЯBCDЮЊЕШЖдНЧЕФЫФБпаЮЕФУцЛ§зюДѓЃПШєДцдкЃЌЪдЧѓГіЫФБпаЮABCDЕФзюДѓУцЛ§ЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉЁЯC=130ЁуЃЛЃЈ2ЃЉжЄУїМћНтЮіЃЛЃЈ3ЃЉSЫФБпаЮABCD=![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉвбжЊЫФБпаЮABCDЪЧЁАЕШЖдНЧЫФБпаЮЁБЃЌЁЯAЁйЁЯCЃЌЁЯA=70ЁуЃЌЁЯB=80ЁуЃЌИљОнЖЈвхМДПЩЧѓЕУЁЯDЕФЖШЪ§ЃЌдйгЩЫФБпаЮФкНЧКЭЖЈРэМДПЩЧѓЕУЁЯCЕФЖШЪ§ЃЛЃЈ2ЃЉСЌНгBDЃЌгЩAB=AD=aЃЌCB=CD=bЃЌЧвaЁйbЃЌПЩЕУЁЯABD=ЁЯADCЃЌЁїABDгыЁїCBDВЛЯрЫЦЃЌМДЁЯAЁйЁЯCЃЌдђПЩжЄЕУНсТлЃЛЃЈ3ЃЉСЌНгBDЃЌгЩЕБЁЯDAB=ЁЯBCD=60ЁуЪБЃЌЫФБпаЮABCDЪЧЁАЕШЖдНЧЫФБпаЮЁБЃЌПЩЕУДЫЪБЕуCдкBDЮЊЯвЕФ![]() ЩЯЃЌМДПЩЕУвЊЪЙЫФБпаЮABCDЕФУцЛ§зюДѓЃЌдђЕуCдкБпBEЩЯЃЌШЛКѓЙ§ЕуDзїDHЁЭABгкЕуHЃЌзїDMЁЭBCгкЕуMЃЌРћгУЙДЙЩЖЈРэЧѓНтМДПЩЧѓЕУД№АИЃЎ
ЩЯЃЌМДПЩЕУвЊЪЙЫФБпаЮABCDЕФУцЛ§зюДѓЃЌдђЕуCдкБпBEЩЯЃЌШЛКѓЙ§ЕуDзїDHЁЭABгкЕуHЃЌзїDMЁЭBCгкЕуMЃЌРћгУЙДЙЩЖЈРэЧѓНтМДПЩЧѓЕУД№АИЃЎ
ЃЈ1ЃЉЁпЫФБпаЮABCDЪЧЁАЕШЖдНЧЫФБпаЮЁБЃЌЁЯAЁйЁЯCЃЌЁЯA=70ЁуЃЌЁЯB=80ЁуЃЌ
ЁрЁЯD=ЁЯB=80ЁуЃЌ
ЁрЁЯC=360ЁуЉ80ЁуЉ80ЁуЉ70Ёу=130ЁуЃЛ
ЃЈ2ЃЉжЄУїЃКШчЭМ2ЃЌСЌНгBDЃЌ
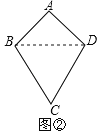
ЁпAB=ADЃЌCB=CDЃЌ
ЁрЁЯABD=ЁЯADBЃЌЁЯCBD=ЁЯCDBЃЌ
ЁрЁЯABD+ЁЯCBD=ЁЯADB+ЁЯCDBЃЌ
ЁрЁЯABC=ЁЯADCЃЌ
ЁпAB=AD=aЃЌCB=CD=bЃЌЧвaЁйbЃЌЧвBD=BDЃЌ
ЁрЁїABDгыЁїCBDВЛЯрЫЦЃЌ
ЁрЁЯAЁйЁЯCЃЌ
ЁрЫФБпаЮABCDЪЧЁАЕШЖдНЧЫФБпаЮЁБЃЎ
ЃЈ3ЃЉШчЭМ3ЃЌСЌНгBDЃЌ
ЕБЁЯDAB=ЁЯBCD=60ЁуЪБЃЌЫФБпаЮABCDЪЧЁАЕШЖдНЧЫФБпаЮЁБЃЌ
ДЫЪБЕуCдкBDЮЊЯвЕФ![]() ЩЯЃЌ
ЩЯЃЌ
вЊЪЙЫФБпаЮABCDЕФУцЛ§зюДѓЃЌдђЕуCдкБпBEЩЯЃЌ
Й§ЕуDзїDHЁЭABгкЕуHЃЌзїDMЁЭBCгкЕуMЃЌ
дкRtЁїADHжаЃЌЁЯDAH=60ЁуЃЌAD=4ЃЌ
ЁрAH=2ЃЌDH=2![]() ЃЌ
ЃЌ
ЁрBH=ABЉAH=4ЃЌ
ЁпЫФБпаТDHBMЪЧОиаЮЃЌ
ЁрBM=DH=2![]() ЃЌDM=BH=4ЃЌ
ЃЌDM=BH=4ЃЌ
дкRtЁїDMCжаЃЌЁЯDCM=60ЁуЃЌ
ЁрCM=![]() DM=
DM=![]() ЃЌ
ЃЌ
ЁрBC=BM+CM=2![]() +
+![]() =
=![]() ЃЌ
ЃЌ
ЁрSЫФБпаЮABCD=SЁїABD+SЁїBCD=![]() ЁС6ЁС2
ЁС6ЁС2![]() +
+![]() ЁС
ЁС![]() ЁС4=
ЁС4=![]() ЃЎ
ЃЎ

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИЁОЬтФПЁПНќФъРДЃЌЁАдкГѕжаЪ§бЇНЬбЇКђзмЪЙгУМЦЫуЦїЪЧЗёжБНггАЯьбЇЩњМЦЫуФмСІЕФЗЂеЙЁБетвЛЮЪЬтЪмЕНСЫЙуЗКЙизЂЃЌЮЊДЫЃЌФГаЃЫцЛњЕїВщСЫnУћбЇЩњЖдДЫЮЪЬтЕФПДЗЈЃЈПДЗЈЗжЮЊШ§жжЃКУЛгагАЯьЃЌгАЯьВЛДѓЃЌгАЯьКмДѓЃЉЃЌВЂНЋЕїВщНсЙћ ЛцжЦГЩШчЯТВЛЭъећЕФЭГМЦБэКЭЩШаЮЭГМЦЭМЃЌИљОнЭГМЦЭМБэЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
nУћбЇЩњЖдЪЙгУМЦЫуЦїгАЯьМЦЫуФмСІЕФЗЂеЙПДЗЈШЫЪ§ЭГМЦБэ
ПДЗЈ | УЛгагАЯь | гАЯьВЛДѓ | гАЯьКмДѓ |
бЇЩњШЫЪ§ЃЈШЫЃЉ | 40 | 60 | m |

ЃЈ1ЃЉЧѓnЕФжЕЃЛ
ЃЈ2ЃЉЭГМЦБэжаЕФm= ЃЛ
ЃЈ3ЃЉЙРМЦИУаЃ1800УћбЇЩњжаШЯЮЊЁАгАЯьКмДѓЁБЕФбЇЩњШЫЪ§ЃЎ