题目内容
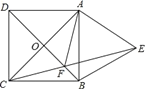
【题目】如图O是正五边形ABCDE的中心,OA=1.
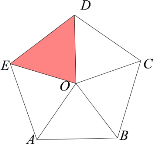
(1)△ODE绕着点 按 方向旋转 度,可以得到△OBC;
(2) △ODE沿 所在直线翻折,可以得到三角形 .
【答案】(1)O,顺时针,144;(或逆时针 216);(2) OD,△ODC.(或OC,△OAB)
【解析】
(1)先计算出正五边形的每各内角的度数,然后找到旋转中心,按照顺时针或逆时针找到一条对应边,看对应边的夹角是多少即可.
(2)根据翻折的性质,图形沿某条直线翻折,翻折后与翻折前图形能够完全重合,依次解决即可.
解:(1)正五边形的每各内角为360÷5=72,即72度,分两种情况讨论:
①△ODE绕着点O按顺时针方向旋转144度,即OE与OC重合,OD与OB,旋转角为∠DOB或∠EOC,可以得到△OBC;
②△ODE绕着点O按逆时针方向旋转216度,即OE与OC重合,OD与OB,可以得到△OBC;
(2)根据翻折的性质,翻折前后图形能够完全重合,即成轴对称,那条直线即为对称轴,可分两种情况:①故△ODE沿OD所在直线翻折,可以得到三角形ODC.
②故△ODE沿OC所在直线翻折,可以得到三角形OAB.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目