Question

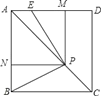
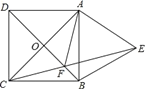
【题目】如图，已知正方形ABCD，以AB为边向外作等边三角形ABE，CE与DB相交于点F，则∠AFD的度数____．

Answer 1

【答案】60°

【解析】

根据正方形及等边三角形的性质求得∠AFE，∠BFE的度数，再根据三角形外角的性质即可求得答案.

解：∵∠CBA=90°，∠ABE=60°，

∴∠CBE=150°，

∵四边形ABCD为正方形，三角形ABE为等边三角形，

∴BC=BE，

∴∠BEC=15°，

∵∠FBE=∠DBA+∠ABE=105°，

∴∠BFE=60°，

在△CBF和△ABF中，

BF＝BF，∠CBF＝∠ABF，BC＝BA，

∴△CBF≌△ABF（SAS），

∴∠BAF=∠BCE=15°，

又∵∠ABF=45°，且∠AFD为△AFB的外角，

∴∠AFD=∠ABF+∠FAB=15°+45°=60°．

故答案为：60°