题目内容
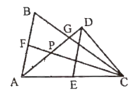
【题目】如图,已知AB=AD,∠ABC=∠ADC.试判断AC与BD的位置关系,并说明理由.

【答案】AC⊥BD,理由见解析.
【解析】
AC与BD垂直,理由为:由AB=AD,利用等边对等角得到一对角相等,利用等式性质得到∠BDC=∠DBC,利用等角对等边得到DC=BC,利用SSS得到三角形ABC与三角形ADC全等,利用全等三角形对应角相等得到∠DAC=∠BAC,再利用三线合一即可得证.
AC⊥BD,理由为:
∵AB=AD(已知),
∴∠ADB=∠ABD(等边对等角),
∵∠ABC=∠ADC(已知),
∴∠ABC﹣∠ABD=∠ADC﹣∠ADB(等式性质),
即∠BDC=∠DBC,
∴DC=BC(等角对等边),
在△ABC和△ADC中,
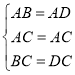
∴△ABC≌△ADC(SSS),
∴∠DAC=∠BAC(全等三角形的对应角相等),
又∵AB=AD,
∴AC⊥BD(等腰三角形三线合一).

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目