题目内容
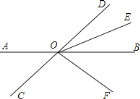
【题目】已知:如图![]() ,点
,点![]() 是线段
是线段![]() 上一定点,
上一定点,![]() ,
,![]() 、
、![]() 两点分别从
两点分别从![]() 、
、![]() 出发以
出发以![]() 、
、![]() 的速度沿直线
的速度沿直线![]() 向左运动,运动方向如箭头所示(
向左运动,运动方向如箭头所示(![]() 在线段
在线段![]() 上,
上,![]() 在线段
在线段![]() 上)
上)
![]() 若
若![]() ,当点
,当点![]() 、
、![]() 运动了
运动了![]() ,此时
,此时![]() ________,
________,![]() ________;(直接填空)
________;(直接填空)
![]() 当点
当点![]() 、
、![]() 运动了
运动了![]() ,求
,求![]() 的值.
的值.
![]() 若点
若点![]() 、
、![]() 运动时,总有
运动时,总有![]() ,则
,则![]() ________(填空)
________(填空)
![]() 在
在![]() 的条件下,
的条件下,![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,求
,求![]() 的值.
的值.
![]()
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() 或
或![]() .
.
【解析】
(1)根据运动速度和时间分别求得CM、BD的长,根据线段的和差计算可得;
(2)由题意得CM=2 cm、BD=4 cm,根据AC+MD=AM﹣CM+BM﹣BD=AB﹣CM﹣BD可得答案;
(3)根据C、D的运动速度知BD=2MC,再由已知条件MD=2AC求得MB=2AM,所以AM=![]() AB;
AB;
(4)分点N在线段AB上时和点N在线段AB的延长线上时分别求解可得.
(1)根据题意知,CM=2cm,BD=4cm.
∵AB=12cm,AM=4cm,∴BM=8cm,∴AC=AM﹣CM=2cm,DM=BM﹣BD=4cm.
故答案为:2,4;
(2)当点C、D运动了2 s时,CM=2 cm,BD=4 cm.
∵AB=12 cm,CM=2 cm,BD=4 cm,∴AC+MD=AM﹣CM+BM﹣BD=AB﹣CM﹣BD=12﹣2﹣4=6 cm;
(3)根据C、D的运动速度知:BD=2MC.
∵MD=2AC,∴BD+MD=2(MC+AC),即MB=2AM.
∵AM+BM=AB,∴AM+2AM=AB,∴AM=![]() AB=4.
AB=4.
故答案为:4;
(4)①当点N在线段AB上时,如图1.

∵AN﹣BN=MN.
又∵AN﹣AM=MN,∴BN=AM=4,∴MN=AB﹣AM﹣BN=12﹣4﹣4=4,∴![]() =
=![]() =
=![]() ;
;
②当点N在线段AB的延长线上时,如图2.

∵AN﹣BN=MN.
又∵AN﹣BN=AB,∴MN=AB=12,∴![]() =
=![]() =1.
=1.
综上所述:![]() =
=![]() 或1.
或1.