题目内容

【题目】如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，AB=10，AD是∠BAC的平分线．若P，Q分别是AD和AC上的动点，则PC+PQ的最小值是（ ）

A. 2.4 B. 4.8 C. 4 D. 5

【答案】B

【解析】

过点C作CM⊥AB交AB于点M，交AD于点P，过点P作PQ⊥AC于点Q，由AD是∠BAC的平分线．得出PQ=PM，这时PC+PQ有最小值，即CM的长度，运用勾股定理求出AB，再运用S△ABC=ABCM=ACBC，得出CM的值，即PC+PQ的最小值．

如图，过点C作CM⊥AB交AB于点M，交AD于点P，过点P作PQ⊥AC于点Q，

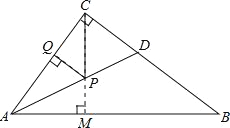
∵AD是∠BAC的平分线.

∴PQ=PM，这时PC+PQ有最小值，即CM的长度,

∵AC=6,BC=8,∠ACB=90°,

∴AB=,

∵=ABCM=ACBC,

∴CM=.

故选：B.

练习册系列答案
相关题目

【题目】最近，“校园安全”受到全社会的广泛关注，重庆一中学生会新闻社准备近期做一个关于“校园安全”的专刊．为了解同学们对“校园安全”知识的了解程度，决定随机抽取部分同学进行一次问卷调查，问卷将了解程度分为（了解）、（了解很少）、（基本了解）、（不了解）四种类型，根据调查结果绘制成了如下两幅不完整的统计图，请结合统计图信息解答下列问题：

（1）这次调查中，一共调查了 名学生，图中类所对应的圆心角度数为 ；

（2）请补全条形统计图；

（3）为了让全校师生都能更好地关注“校园安全”，学生会准备组织一次宣讲活动，由问卷调查中“了解”的几名同学组成一个宣讲团．已知这几名同学中有四名来自初一，其中两名为男生；另外四名来自初二，其中一名为女生．若要在该宣讲团中分别抽取初一、初二各一名同学在全校师生大会上作代表发言，请用列表法或画树状图的方法求出恰好抽到一名男生和一名女生来发言的概率．

【题目】中学生上学带手机的现象越来越受到社会的关注，为此媒体记者随机调查了某校若干名学生上学带手机的目的，分为四种类型：A接听电话；B收发短信；C查阅资料；D游戏聊天．并将调查结果绘制成图1和图2的统计图（不完整），请根据图中提供的信息，解答下列问题：

（1）此次抽样调查中，共调查了 名学生.
（2）将图1、图2补充完整；
（3）现有4名学生，其中A类两名，B类两名，从中任选2名学生，求这两名学生为同一类型的概率（用列表法或树状图法）．

【题目】张华在一次数学活动中，利用“在面积一定的矩形中，正方形的周长最短”的结论，推导出“式子x+ （x＞0）的最小值是2”．其推导方法如下：在面积是1的矩形中设矩形的一边长为x，则另一边长是 ，矩形的周长是2（x+ ）；当矩形成为正方形时，就有x= （x＞0），解得x=1，这时矩形的周长2（x+ ）=4最小，因此x+ （x＞0）的最小值是2．模仿张华的推导，你求得式子 （x＞0）的最小值是（ ）
A.2
B.1
C.6
D.10

【题目】学习成为现代人的时尚，某市有关部门统计了最近6个月到图书馆的读者的职业分布情况，并做了下列两个不完整的统计图．
（1）在统计的这段时间内，共有万人次到图书馆阅读，其中商人占百分比为%；
（2）将条形统计图补充完整；
（3）若5月份到图书馆的读者共28000人次，估计其中约有多少人次读者是职工？

【题目】数学活动课上，老师准备了若干个如图1的三种纸片，A种纸片边长为a的正方形，B种纸片是边长为b的正方形，C种纸片长为a、宽为b的长方形．并用A种纸片一张，B种纸片张，C种纸片两张拼成如图2的大正方形．

（1）请用两种不同的方法求图2大正方形的面积．

方法1：　 　；方法2：　 　

（2）观察图2，请你写出下列三个代数式：（a+b）2，a2+b2，ab之间的等量关系．　 　

（3）根据（2）题中的等量关系，解决如下问题：

①已知：a+b=5，a2+b2=11，求ab的值；

②已知（2018﹣a）2+（a﹣2017）2=5，求（2018﹣a）（a﹣2017）的值．

【题目】二次函数图象的顶点在原点O，经过点A（1， ）；点F（0，1）在y轴上．直线y=﹣1与y轴交于点H．

（1）求二次函数的解析式；
（2）点P是（1）中图象上的点，过点P作x轴的垂线与直线y=﹣1交于点M，求证：FM平分∠OFP；
（3）当△FPM是等边三角形时，求P点的坐标．

【题目】判断正误，并说明理由(1)给定一组数据，那么这组数据的众数有可能不唯一________；理由________(2)给定一组数据，那么这组数据的平均数一定是这组数据中的一个数________；

理由________(3)n个数的中位数一定是这n个数中的某一个________；理由________(4)求9个数据（x1、x2、……、x9 ， 其平均数为m）的标准差S， 计算公式为： ________；理由________

【题目】开学初，小芳和小亮去学校商店购买学习用品，小芳用30元钱购买钢笔的数量是小亮用25元钱购买笔记本数量的2倍，已知每支钢笔的价格比每本笔记本的价格少2元

（1）求每支钢笔和每本笔记本各是多少元；

（2）学校运动会后，班主任再次购买上述价格的钢笔和笔记本共50件作为奖品，奖励给校运动会中表现突出的同学，总费用不超过200元．请问至少要买多少支钢笔？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网