题目内容
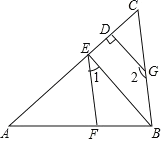
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=50°,点D在线段BC上运动(点D不与B,C重合),连接AD,作∠ADE=50°,DE交线段AC于点E.

(1)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请求出∠BDA的度数;若不可以,请说明理由.
(2)若DC=2,求证:△ABD≌△DCE.
【答案】(1)100°或115°(2)证明见解析
【解析】
(1)分两种情况进行讨论,根据三角形的外角性质,可得当∠BDA的度数为115°或100°时,△ADE的形状是等腰三角形;
(2)利用∠DEC+∠EDC=130°,∠ADB+∠EDC=130°,求出∠ADB=∠DEC,再利用AB=DC=2,即可得出△ABD≌△DCE.
(1)△ADE的形状可以是等腰三角形
∵∠B=∠C=50°,∠ADE=50°,
∴∠BDA+∠EDC=∠CED+∠EDC=130°,
∴∠BDA=∠CED.
∵点D在线段BC上运动(点D不与B,C重合),
∴AD≠AE.
当EA=ED时,如图1所示,∠EAD=∠ADE=50°,
∴∠BDA=∠CED=50°+50°=100°;
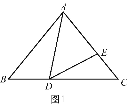
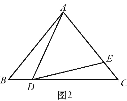
当DA=DE时,如图2所示,∠EAD=∠AED=65°,
∴∠BDA=∠CED=65°+50°=115°.
综上,∠BDA为100°或115°.
(2) ∵DC=2, AB=AC=2,
∴AB=DC
由(1)可得∠BDA=∠CED,
在△ABD和△DCE中,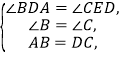
∴△ABD≌△DCE(AAS).

【题目】某校举办“红歌伴我成长”歌咏比赛活动,参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如图:
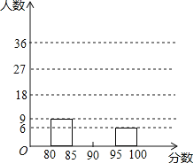
分数段 | 频数 | 频率 |
80≤x<85 | 9 | 0.15 |
85≤x<90 | m | 0.45 |
90≤x<95 | ■ | ■ |
95≤x<100 | 6 | n |
(1)求m,n的值分别是多少;
(2)请在图中补全频数分布直方图;
(3)比赛成绩的中位数落在哪个分数段?