��Ŀ����
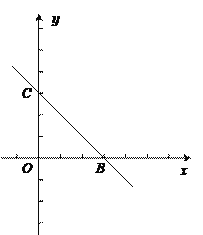
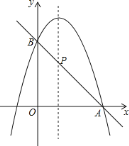
����Ŀ��ij������Ʒ�̵�����һ��ɱ�Ϊ50Ԫ���������涨�����ڼ䵥�۲����ڳɱ������һ������ø���40%��������������������y�����������۵���x��Ԫ��֮��������ͼ��ʾ��һ�κ�����ϵ��
��1����ȷ��y��x֮��ĺ�����ϵʽ��
��2������������Ʒ�̵������������������õ�����QԪ����д������Q��Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ�����������۶�Ϊ����Ԫʱ�����̵�ɻ����������������Ƕ���Ԫ��
��3�������̵����������������õ�������600Ԫ����ȷ�����۵���x��ȡֵ��Χ��
���𰸡���1�� y����x��120����2�� Q����x2+170x��6000�����������۶�Ϊ70Ԫʱ�����̵�ɻ�������������������1000Ԫ����3������Ϊ60��x��70��������
��������
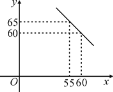
��1�����ô���ϵ������ͼ�е���������һ�κ�������ʽ������
��2�����������ۼ۩��ɱ������������г�������ϵʽ��
��3�������ϵʽQ��600�����x�ķ�Χ�����á��������ø���40%�����x�����ֵ���ó����۵���x�ķ�Χ��
��1����y��kx+b�������������
![]()
�����k����1��b��120��
����һ�κ����ı���ʽΪy����x+120��
��2������Q�����۵���x֮��ĺ�����ϵʽΪ��Q����x��50������x+120������x2+170x��6000��Q����x2+170x��6000������x��85��2+1225��
�߳ɱ�Ϊ50Ԫ���������涨�����ڼ䵥�۲����ڳɱ������һ������ø���40%����50��x��70���൱�������۶�Ϊ70Ԫʱ�����̵�ɻ�������������������1000Ԫ��
��3�������������x2+170x��6000��600�������60��x��110��
�������ø���40%������۸�Ϊ50��1+40%����70�������۵���x��ȡֵ��Χ��60��x��70��������

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�