题目内容
【题目】【感受联系】在初二的数学学习中,我们感受过等腰三角形与直角三角形的密切联系.等腰三角形作底边上的高线可转化为直角三角形,直角三角形沿直角边翻折可得到等腰三角形等等.
(1)【探究发现】某同学运用这一联系,发现了“30°角所对的直角边等于斜边的一半”.并给出了如下的部分探究过程,请你补充完整证明过程
已知:如图,
在 ![]() △
△![]() 中,
中, ![]() °,
°, ![]() °.
°.
求证: ![]() .
.
(2)【灵活运用】该同学家有一张折叠方桌如图①所示,方桌的主视图如图②.经测得 ![]() ,
, ![]() ,将桌子放平,两条桌腿叉开的角度
,将桌子放平,两条桌腿叉开的角度 ![]() .
.
求:桌面与地面的高度.
【答案】
(1)证明:取AB的中点D,连接CD,
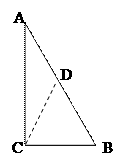
∵在Rt△ABC中,点D是AB的中点,
∴CD=DB= ![]() AB ,
AB ,
∵∠C=90°,∠A=30°,
∴∠B=60°,
∴△DBC是等边三角形 ,
∴BC=CD=DB,
∴BC= ![]() AB
AB
(2)解:过O作,OE⊥AB于E,OF⊥CD于点F,
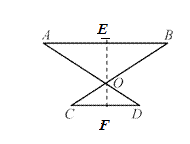
∵OA=OB,∠AOB=120°,
∴∠A=30° ,
在Rt△AOE中,OA=90,∠A=30°, ![]() ,
,
∴OE=45 ,
同理:OF=15.
所以,桌面与地面的高度是60cm.
【解析】(1)根据在直角三角形中,斜边上的中线是斜边的一半;得到CD=DB=![]() AB;根据三角形内角和定理求出∠B=60°,得到△DBC是等边三角形 ,得到BC=CD=DB,得到BC=
AB;根据三角形内角和定理求出∠B=60°,得到△DBC是等边三角形 ,得到BC=CD=DB,得到BC=![]() AB;(2)根据等腰三角形的性质,得到∠A=30° ,根据在直角三角形中,30度角所对的边是斜边的一半;得到OE=
AB;(2)根据等腰三角形的性质,得到∠A=30° ,根据在直角三角形中,30度角所对的边是斜边的一半;得到OE=![]() OB,同理OF=
OB,同理OF=![]() OC,求出桌面与地面的高度.
OC,求出桌面与地面的高度.
【考点精析】解答此题的关键在于理解含30度角的直角三角形的相关知识,掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半,以及对直角三角形斜边上的中线的理解,了解直角三角形斜边上的中线等于斜边的一半.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
