题目内容
【题目】如图,在平面直角坐标系xOy中,菱形ABCD的对角线AC与BD交于点P(-1,2),AB⊥x轴于点E,正比例函数y=mx的图像与反比例函数![]() 的图像交于A,P两点.
的图像交于A,P两点.
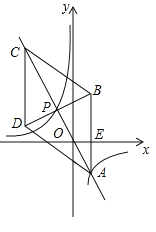
(1)求m,n的值与点A的坐标
(2)求![]() 的值
的值
【答案】(1)m=﹣2,n=1,点A的坐标为(1,﹣2);(2)![]()
【解析】
(1)根据点P的坐标,利用待定系数法可求出m,n的值,联立正、反比例函数解析式成方程组,通过解方程组可求出点A的坐标(利用正、反比例函数图象的对称性结合点P的坐标找出点A的坐标亦可);
(2)由点A的坐标可得出AE,OE,AO的长,由相似三角形的性质可得出∠CDP=∠AOE,再利用正弦的定义即可求出sin∠CDB的值.
(1)解:将点P(-1,2)代入y=mx,得:2=-m,
解得:m=-2,
∴正比例函数解析式为y=-2x;
将点P(-1,2)代入y=![]() ,得:2=-(n-3),
,得:2=-(n-3),
解得:n=1,
∴反比例函数解析式为y=-![]() .
.
联立正、反比例函数解析式成方程组,得: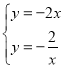 ,
,
解得: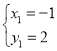 ,
,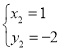 ,
,
∴点A的坐标为(1,-2).
(2)解:∵点A的坐标为(1,-2),
∴AE=2,OE=1,AO=![]() .
.
∵四边形ABCD是菱形,
∴AC⊥BD,AB∥CD,
∴∠DCP=∠BAP,即∠DCP=∠OAE.
∵AB⊥x轴,
∴∠AEO=∠CPD=90°,
∴△CPD∽△AEO,
∴∠CDP=∠AOE,
∴sin∠CDB=sin∠AOE=![]() .
.

【题目】如图,漏壶是一种古代计时器.在它内部盛一定量的水,水从壶下的小孔漏出.壶内壁有刻度,人们根据壶中水面的位置计算时间.用x(小时)表示漏水时间,y(厘米)表示壶底到水面的高度,某次计时过程中,记录到部分数据如下表:
漏水时间x(小时) | … | 3 | 4 | 5 | 6 | … |
壶底到水面高度y(厘米) | … | 9 | 7 | 5 | 3 | … |
(1)问y与x的函数关系属于一次函数、二次函数和反比例函数中的哪一种?求出该函数解析式及自变量x的取值范围;
(2)求刚开始计时时壶底到水面的高度.