题目内容
【题目】已知⊙O的半径为2,A为圆内一定点,AO=1.P为圆上一动点,以AP为边作等腰△APG,AP=PG,∠APG=120°,OG的最大值为( )

A.1+![]() B.1+2
B.1+2![]() C.2+
C.2+![]() D.2
D.2![]() ﹣1
﹣1
【答案】B
【解析】
如图,将线段OA绕点O顺时针旋转120°得到线段OT,连接AT,GT,OP.则AO=OT=1,AT=![]() ,利用相似三角形的性质求出GT,再根据三角形的三边关系解决问题即可.
,利用相似三角形的性质求出GT,再根据三角形的三边关系解决问题即可.
解:如图,将线段OA绕点O顺时针旋转120°得到线段OT,连接AT,GT,OP.则AO=OT=1,AT=![]() ,
,
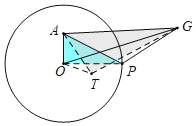
∵△AOT,△APG都是顶角为120°的等腰三角形,
∴∠OAT=∠PAG=30°,
∴∠OAP=∠TAG,![]()
∴![]() ,
,
∴△OAP∽△TAG,
∴![]() ,∵OP=2,
,∵OP=2,
∴TG=2![]() ,
,
∵OG≤OT+GT,
∴OG≤1+2![]() ,
,
∴OG的最大值为1+2![]() ,
,
故选:B.

练习册系列答案
相关题目