题目内容
【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠B=60°.
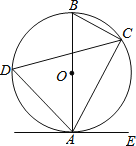
(1)求∠ADC的度数;
(2)求证:AE是⊙O的切线.
【答案】(1)60° (2)见解析
【解析】
试题(1)根据“同弧所对的圆周角相等”可以得到∠ADC=∠B=60°。
(2)欲证明AE是⊙O的切线,只需证明BA⊥AE即可。
解:(1)∵∠B与∠ADC都是弧AC所对的圆周角,∠B=60°,
∴∠ADC=∠B=60°。
(2)证明:∵AB是⊙O的直径,∴∠ACB=90°。
∵∠B=60°,∴∠BAC=30°。
又∵∠EAC =60°,∴∠BAE=∠BAC+∠EAC=30°+60°=90°,即 BA⊥AE。
又∵AB是⊙O的直径,∴AE是⊙O的切线。

【题目】某公司欲招聘一名部门经理,对甲、乙、丙三名候选人进行了笔试与面试,甲、乙、丙三人的笔试成绩分别为95分、94分和94分.他们的面试成绩如表:
候选人 | 评委1 | 评委2 | 评委3 |
甲 | 94 | 89 | 90 |
乙 | 92 | 90 | 94 |
丙 | 91 | 88 | 94 |
(1)分别求出甲、乙、丙三人的面试成绩的平均分![]() 、
、![]() 、和
、和![]() ;
;
(2)若按笔试成绩的40%与面试成绩的60%的和作为综合成绩,综合成绩高者将被录用,请你通过计算判断谁将被录用.
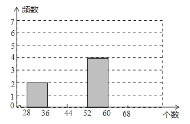
【题目】阳泉同学参加周末社会实践活动,到“富乐花乡”蔬菜大棚中收集到20株西红柿秧上小西红柿的个数:32、39、45、55、60、54、 60、28、56、41、51、36、44、46、40、53、37、47、45、46.
(1)前10株西红柿秧上小西红柿个数的平均数是多少?中位数是多少?众数是多少?
(2)若对这20个数按组距为8进行分组,请补全频数分布表及频数分布直方图
个数分组 | 28≤x<36 | 36≤x<44 | 44≤x<52 | 52≤x<60 | 60≤x<68 |
频数 | 2 |
|
|
| 2 |
(3)通过频数分布直方图试分析此大棚中西红柿的长势.