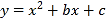题目内容
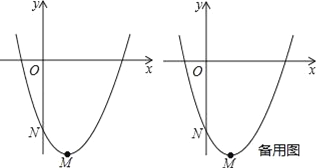
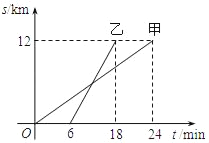
【题目】如图，甲、乙两人以相同路线前往离学校12千米的地方参加植树活动．分析甲、乙两人前往目的地所行驶的路程S（千米）随时间t（分钟）变化的函数图象，解决下列问题：
（1）求出甲、乙两人所行驶的路程S甲、S乙与t之间的关系式；
（2）甲行驶10分钟后，甲、乙两人相距多少千米？
【答案】（1）S甲=0.5t；S乙=t﹣6；（2）甲行驶10分钟后，甲、乙两人相距1千米；
【解析】
设出函数解析式，用待定系数法求解即可.
代入中的函数解析式即可求出.
（1）由图象设甲的解析式为：S甲=kt，代入点
，解得：k=0.5；
所以甲的解析式为：S甲=0.5t；
同理可设乙的解析式为：S乙=mt+b，代入点
可得：
解得：
，
所以乙的解析式为S乙
（2）当t=10时，S甲=0.5×10=5（千米），S乙=10-6=4（千米），
5-4=1（千米），
答：甲行驶10分钟后，甲、乙两人相距1千米．
口算心算速算应用题系列答案
同步拓展阅读系列答案
【题目】某校召开运动会，七（1）班学生到超市分两次（第二次少于第一次）购买某种饮料90瓶，共用去205元，已知该种饮料价格如下：
购买瓶数/瓶 | 不超过30 | 30以上不超过50 | 50以上 |
单价/元 | 3 | 2.5 | 2 |
求：两次分别购买这种饮料多少瓶？
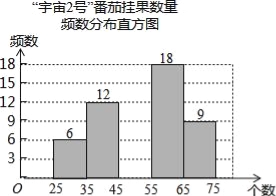
【题目】在太空种子种植体验实践活动中，为了解“宇番2号”番茄，某校科技小组随机调查60株番茄的挂果数量x（单位：个），并绘制如下不完整的统计图表：
“宇番2号”番茄挂果数量统计表
挂果数量x（个） | 频数（株） | 频率 |
25≤x＜35 | 6 | 0.1 |
35≤x＜45 | 12 | 0.2 |
45≤x＜55 | a | 0.25 |
55≤x＜65 | 18 | b |
65≤x＜75 | 9 | 0.15 |
请结合图表中的信息解答下列问题：
（1）统计表中，a= ，b= ；
（2）将频数分布直方图补充完整；
（3）若绘制“番茄挂果数量扇形统计图”，则挂果数量在“35≤x＜45”所对应扇形的圆心角度数为 °；
（4）若所种植的“宇番2号”番茄有1000株，则可以估计挂果数量在“55≤x＜65”范围的番茄有 株．
