题目内容
【题目】仔细想一想,完成下面的说理过程.
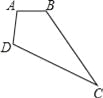
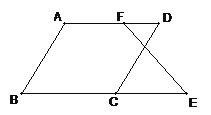
如图,已知AB∥CD,∠B=∠D
求证:∠E=∠DFE.
证明:∵AB∥CD (已知 ),
∴∠B+∠ =180°( )
又∵∠B=∠D(已知 )
∴∠D +∠BCD=180°( )
∴ ( )
∴∠E=∠DFE( )
【答案】BCD;两直线平行,同旁内角互补;等量代换;AD∥BE;同旁内角互补,两直线平行;两直线平行,内错角相等.
【解析】
由AB∥CD根据两直线平行,同旁内角互补可得∠B+∠BCD =180°,再结合题中条件等量代换可根据同旁内角互补,两直线平行证得AD∥BE,由两直线平行,内错角相等可得结论.
解:证明:∵AB∥CD (已知)
∴∠B+∠BCD =180°( 两直线平行,同旁内角互补)
又∵∠B=∠D(已知 )
∴∠D +∠BCD=180°(等量代换)
∴AD∥BE(同旁内角互补,两直线平行)
∴∠E=∠DFE(两直线平行,内错角相等)

练习册系列答案
相关题目
【题目】弹簧挂上物体后会伸长,若一弹簧长度(cm)与所挂物体质量(kg)之间的关系如下表:
物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
则下列说法错误的是( )
A.弹簧长度随物体的质量的变化而变化,物体的质量是自变量,弹簧的长度是因变量
B.如果物体的质量为x kg,那么弹簧的长度y cm可以表示为y=12+0.5x
C.在弹簧能承受的范围内,当物体的质量为7kg时,弹簧的长度为16cm
D.在没挂物体时,弹簧的长度为12cm